本文介绍卷积神经网络（CNN），涵盖其包含的卷积层、ReLU层等各类层及相关运算、参数计算等，还讲解激活函数、BatchNorm层、Dropout，列举LeNet等经典网络，提及CNN改进思路，从优化指标和通用方法等方面阐述如何优化CNN。
☞☞☞AI 智能聊天, 问答助手, AI 智能搜索, 免费无限量使用 DeepSeek R1 模型☜☜☜
卷积神经网络CNN
卷积神经网络通常包含以下几种层：
卷积层（Convolutional layer），卷积神经网路中每层卷积层由若干卷积单元组成，每个卷积单元的参数都是通过反向传播算法优化得到的。卷积运算的目的是提取输入的不同特征，第一层卷积层可能只能提取一些低级的特征如边缘、线条和角等层级，更多层的网络能从低级特征中迭代提取更复杂的特征。
线性整流层（Rectified Linear Units layer, ReLU layer），这一层神经的活性化函数（Activation function）使用线性整流（Rectified Linear Units, ReLU）f(x)=max(0,x)f(x)=max(0,x)。
池化层（Pooling layer），通常在卷积层之后会得到维度很大的特征，将特征切成几个区域，取其最大值或平均值，得到新的、维度较小的特征。
全连接层（ Fully-Connected layer）, 把所有局部特征结合变成全局特征，用来计算最后每一类的得分。
一、卷积层
1. 卷积
2. 卷积（Convolution)运算
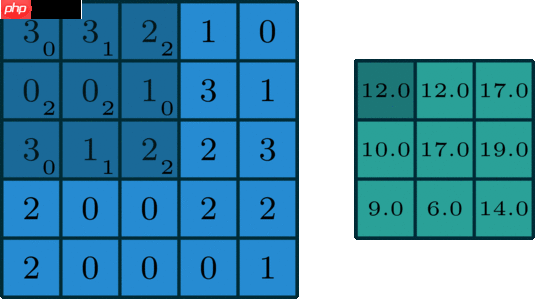
以5x5的矩阵为例：这里我们使用3x3的卷积核（无填充，步长为1）进行卷积运算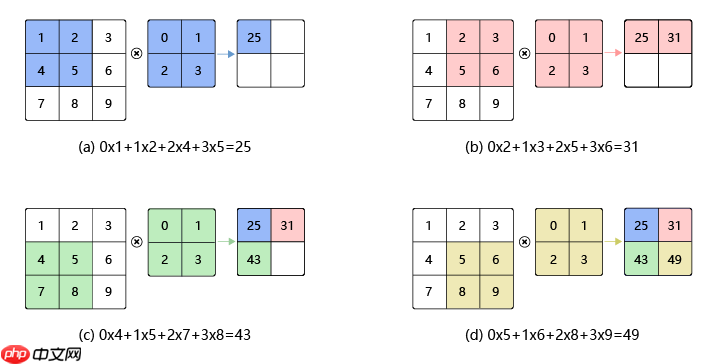 
--
-- 卷积核为： [0,1,2,
2,2,0,
0,1,2]
其中第一个12的计算过程为3x0+3x1+2x2+
0x2+0x2+1x0+
3x0+1x1+2x2=0+3+4+0+0+0+0+1+4=12
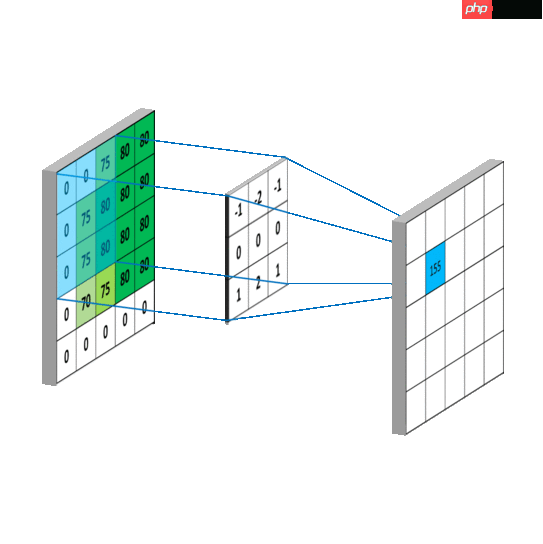
3. 填充
4. 步长
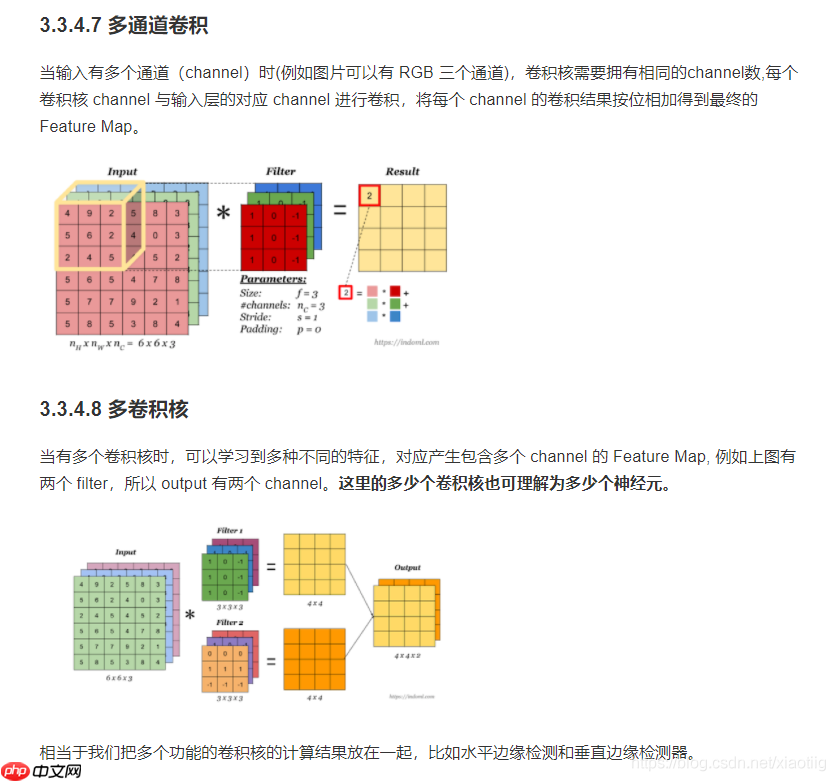
5. 多通道卷积和多卷积核
6. 卷积参数计算
7. 设计卷积
8. 代码实现
# 简化计算，假设batchsize为1， 卷积核个数为1import numpy as np# 滑窗实现class Conv2d(object):
def __init__(self, img, c_out, kernel, stride, padding):
self.img = img
self.c_out = c_out
self.kernel = kernel
self.stride = stride
self.padding = padding def conv(self):
input_c, input_h, input_w = self.img.shape # out_ = []
# for c_o in range(self.c_out):
output = [] #分通道划窗计算
for c in range(input_c):
out = self.compute_conv(input[c], self.kernel[c])
output.append(out) # out_.append(sum(output))
return sum(output) def compute_conv(self, input_c, kernel_c):
k, _ = kernel_c.shape
h, w = input_c.shape if self.padding == "valid":
out_h = (h - k)//self.stride + 1
out_w = (w - k)//self.stride + 1
pad_h, pad_w = 0, 0
if self.padding == "same":
out_h, out_w = h, w
pad_w = (w*(self.stride-1)+k-self.stride)//2
pad_h = (h*(self.stride-1)+k-self.stride)//2
if self.padding == "full":
pad_w = k-1
pad_h = k-1
out_h = (w + 2*pad_h - k) // self.stride + 1
out_w = (h + 2*pad_w - k) // self.stride + 1
input_padding = np.zeros((h+pad_h*2, w+pad_w*2))
input_padding[pad_h:pad_h+h, pad_w:pad_w+w] = input_c
out = np.zeros((out_h, out_w)) for i in range(0, out_h): for j in range(0, out_w):
out[i, j] = np.sum(input_padding[i*self.stride:i*self.stride+k, j*self.stride:j*self.stride+k] * kernel_c) return out# 矩阵实现class Conv2dMatrix():
def __init__(self, img, c_out, kernel, stride, padding):
self.img = img
self.c_out = c_out
self.kernel = kernel
self.stride = stride
self.padding = padding def conv(self):
c, h, w = self.img.shape
c_k, k, _ = self.kernel.shape if self.padding == "same":
out_h, out_w = h, w
pad_w = (self.stride*(w-1) - w + k) // 2
pad_h = (self.stride*(h-1) - h + k) // 2
if self.padding == "valid":
out_h = (h-k) // self.stride + 1
out_w = (w-k) // self.stride + 1
pad_h = 0
pad_w = 0
if self.padding == "full":
pad_w = k - 1
pad_h = k - 1
out_h = (h + 2*pad_h - k) // self.stride + 1
out_w = (w + 2*pad_w - k) // self.stride + 1
img_padding = np.zeros((c, h+2*pad_h, w+2*pad_w))
img_padding[:, pad_h:pad_h+h, pad_w:pad_w+w] = self.img
feature_matrix = np.zeros((out_w*out_h, c_k*k*k))
patch = 0
for i in range(out_h): for j in range(out_w):
feature_patch = img_padding[:, i*self.stride:i*self.stride+k, j*self.stride:j*self.stride+k]
feature_matrix[patch] = feature_patch.flatten()
patch += 1
kernel_matrix = self.kernel.reshape(c_k*k*k, 1) return np.dot(feature_matrix, kernel_matrix).reshape(out_h, out_w)input = np.array([[[1, 2, 3, 4, 5]]*5])print("input=",input,"\n")input = input.reshape(-1, input.shape[1], input.shape[2])
kernel = np.array([[[0, 1, 1], [1, 0, 1], [1, 0, 0]]])
kernel = kernel.reshape(-1, kernel.shape[1], kernel.shape[2])
conv2d = Conv2d(input, 1, kernel, 1, padding="valid")
out1 = conv2d.conv()print("out1=",out1,"\n")print("==============================================\n")
conv2d_m = Conv2dMatrix(input, 1, kernel, 1, padding='valid')
out2 = conv2d_m.conv()print("out2=",out2,"\n")
input= [[[1 2 3 4 5] [1 2 3 4 5] [1 2 3 4 5] [1 2 3 4 5] [1 2 3 4 5]]] out1= [[10. 15. 20.] [10. 15. 20.] [10. 15. 20.]] ============================================== out2= [[10. 15. 20.] [10. 15. 20.] [10. 15. 20.]]
二、池化层(Pooling Layer)
池化（pool）即下采样（downsamples），目的是为了减少特征图。池化操作对每个深度切片独立，规模一般为 2＊2，相对于卷积层进行卷积运算，池化层进行的运算一般有以下几种：
- 最大池化（Max Pooling）。取4个点的最大值。这是最常用的池化方法。
- 均值池化（Mean Pooling）。取4个点的均值。
- 高斯池化。借鉴高斯模糊的方法。不常用。
- 可训练池化。训练函数 ff ，接受4个点为输入，出入1个点。不常用。
最常见的池化层是规模为2*2， 步幅为2，对输入的每个深度切片进行下采样。每个MAX操作对四个数进行，如下图所示：
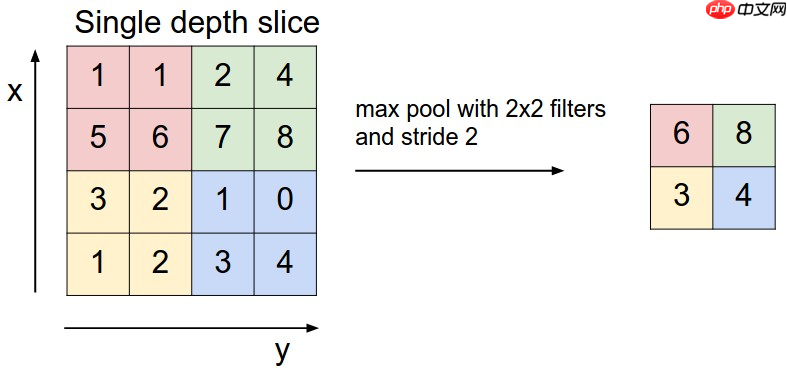
池化操作将保存深度大小不变。
如果池化层的输入单元大小不是二的整数倍，一般采取边缘补零（zero-padding）的方式补成2的倍数，然后再池化。
池化层总结(Summary)
接收单元大小为：W1∗H1∗D1 需要两个参数（hyperparameters）： their spatial extent F, the stride S, 输出大小：W2∗H2∗D2，其中： W2=(W1−F)/S+1
H2=(H1−F)S+1
D2=D1
不需要引入新权重
import numpy as np
input = np.array([
[1,2,1,1],
[0,1,2,1],
[1,1,0,1],
[3,0,0,1]])
k = np.array([
[0,1,0],
[0,1,0],
[0,1,0]])
h,w = input.shape
conv = [] # 卷积操作max_pool = [] # 最大池化ave_pool = [] # 平均池化
for i in range(h-2):
line_conv = [] for j in range(w-2):
t = input[i:i+3,j:j+3]
line_conv.append(np.sum(k*t)) # 输入3×3区域和卷积核进行对应元素相乘再相加
conv.append(line_conv)
for i in range(0,w,2):
line_ave = []
line_max = [] for j in range(0,h,2):
t = input[i:i+2,j:j+2]
line_ave.append(np.sum(t)/4)
line_max.append(np.max(t)) # 注意, 要用np.max(), 不是max()
ave_pool.append(line_ave)
max_pool.append(line_max)
print('conv = \n',conv,'\nmax_pool = \n',max_pool,'\nave_pool = \n',ave_pool)
conv = [[4, 3], [2, 2]] max_pool = [[2, 2], [3, 1]] ave_pool = [[1.0, 1.25], [1.25, 0.5]]
三、全连接层（Fully-connected layer）
全连接层和卷积层可以相互转换：
- 对于任意一个卷积层，要把它变成全连接层只需要把权重变成一个巨大的矩阵，其中大部分都是0 除了一些特定区块（因为局部感知），而且好多区块的权值还相同（由于权重共享）。
- 相反地，对于任何一个全连接层也可以变为卷积层。比如，一个K＝4096的全连接层，输入层大小为 7∗7∗512，它可以等效为一个 F=7, P=0, S=1, K=4096 的卷积层。换言之，我们把 filter size 正好设置为整个输入层大小。
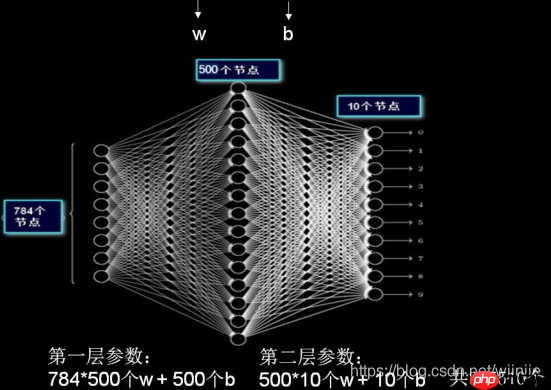
四、激活函数
1. Sigmoid 函数也叫 Logistic 函数，定义为：
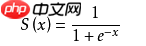
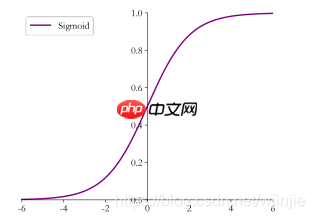
作为激活函数，将输入映射到0~1，因此可以通过 Sigmoid 函数将输出转译为概率输出，常用于表示分类问题的事件概率。 导数性质：在输入x=0时，导数最大为0.25；当输入为正负无穷时，梯度趋于0，会发生梯度弥散。 优点：平滑、易于求导 缺点：指数级计算，计算量大；容易出现梯度弥散的情况。
2. Tanh
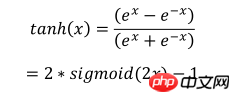
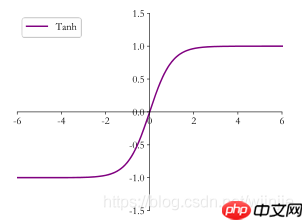Tanh 函数能够将输入x映射到[−1,1]区间。是Sigmoid函数的改进版，输出有正有负，是以0为中心的对称函数，收敛速度快，不容易出现loss值震荡。但是无法解决梯度弥散问题，同时计算量也大
3. ReLU
在 ReLU(REctified Linear Unit，修正线性单元)激活函数提出之前，Sigmoid 函数通常是神经网络的激活函数首选。但是 Sigmoid 函数在输入值较大或较小时容易出现梯度弥散现象，网络参数长时间得不到更新，很难训练较深层次的网络模型。2012 年提出的 8 层 AlexNet 采用了一种名叫 ReLU 的激活函数，使得网络层数达到了 8 层。ReLU 函数定义为：ReLU(x) = max(0, x)
ReLU 对小于 0 的值全部抑制为 0；对于正数则直接输出，这种单边抑制特性来源于生物学。其函数曲线如下：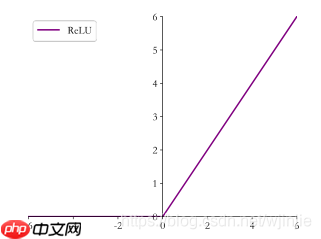 
优点： (1) 使训练快速收敛，解决了梯度弥散。在信息传递的过程中，大于0的部分梯度总是为1。 (2) 稀疏性：模拟神经元的激活率是很低的这一特性；ReLU的输入在大于0时才能传播信息，正是这样的稀疏性提高了网络的性能。
缺点：在输入小于0的时候，即使有很大的梯度传播过来也会戛然而止。
4. Leaky ReLU
ReLU 函数在输入x
其中p为用户自行设置的某较小数值的超参数，如 0.02 等。当p = 0时，LeayReLU 函数退化为 ReLU 函数。当p ≠ 0时，x
5. Softmax
Softmax 函数定义：
Softmax 函数不仅可以将输出值映射到[0,1]区间，还满足所有的输出值之和为 1 的特性。如下图的例子，输出层的输出为[2.,1.,0.1]，经过 Softmax 函数计算后，得到输出为[0.7,0.2,0.1]，可以看到每个值代表了当前样本属于每个类别的概率，概率值之和为 1。
通过 Softmax 函数可以将输出层的输出转译为类别概率，在多分类问题中使用的非常频繁。 另外，在softmax函数多分类问题中，若损失函数选用交叉熵，则下降梯度计算起来将会非常方便，使得网络训练过程中的迭代计算复杂度大大降低。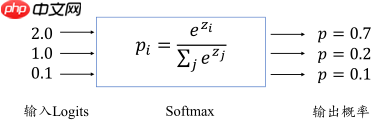 
6. Softplus
函数定义为：f(x)=ln(1+e^x)，值域为（0，+无穷），其图像如下图所示：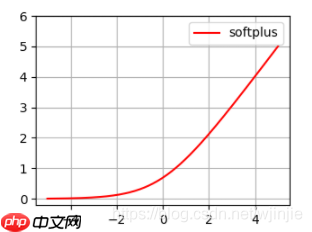 
softplus可以看作是ReLu的平滑。根据神经科学家的相关研究，softplus和ReLu与脑神经元激活频率函数有神似的地方。也就 是说，相比于早期的激活函数，softplus和ReLU更加接近脑神经元的激活模型。
7. Mish
在YOLOv3中，每个卷积层之后包含一个批量归一化层和一个Leaky ReLU。而在YOLOv4的主干网络CSPDarknet53中，使用Mish代替了原来的Leaky ReLU。Leaky ReLU和Mish激活函数的公式与图像如下：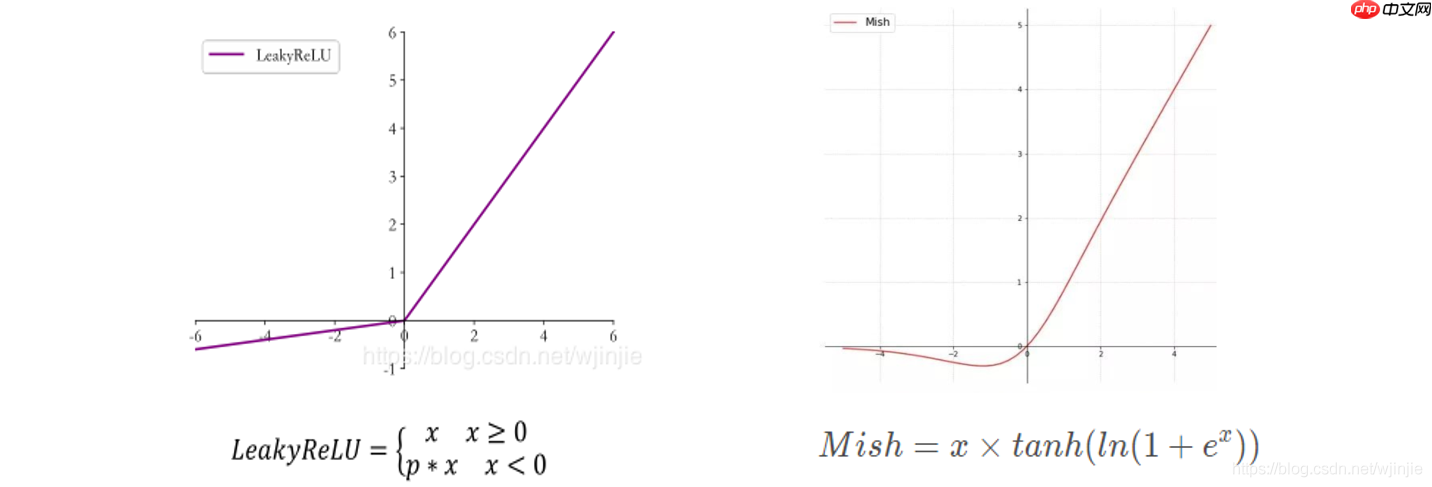
常见的激活函数总结： 
五、BatchNorm(BN)层
1. 背景
卷积神经网络的出现，网络参数量大大减低，使得几十层的深层网络成为可能。然而，在残差网络出现之前，网络的加深使得网络训练变得非常不稳定，甚至出现网络长时间不更新或者不收敛的情形，同时网络对超参数比较敏感，超参数的微量扰动也会导致网络的训练轨迹完全改变。
2. 提出
2015 年，Google 研究人员Sergey Ioffe等提出了一种参数标准化(Normalize)的手段，并基于参数标准化设计了 Batch Nomalization(简称 BatchNorm或 BN)层 。BN层提出后： （1）使得网络的超参数的设定更加自由，比如更大的学习率，更随意的网络初始化等，同时网络的收敛速度更快，性能也更好。 （2）广泛地应用在各种深度网络模型上，卷积层、BN 层，ReLU 层、池化层一度成为网络模型的标配单元，通过堆叠 Conv-BN-ReLU-Pooling 方式往往可以获得不错的模型性能。
3. 原理
网络层的输入x分布相近，并且分布在较小范围内时(如 0 附近)，更有利于函数的迭代优化。那么如何保证输入x的分布相近呢？ 数据标准化可以实现此目的，通过数据标准化操作可以将数据x映射x ^：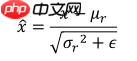 
其中Ur,6r^2来自统计的所有数据x的均值和方差，ϵ是为防止出现除 0的错误而设置的较小数，比如ϵ=1e−8。 很容易很看出来：上面的公式表示的是正太分布。也就是说，通过上面的公式计算，可以将原本随机分布的输入数据x，转化成按正太分布分布的数据x^ ，从而使得输入网络的数据分布较近，有利于网络的迭代优化。
4. 计算
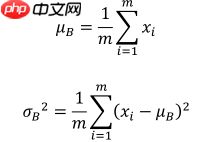
5. Scale and Shift
上述的标准化运算并没有引入额外的待优化变量，μB、δB^2均由统计得到，不需要参与梯度更新。实际上，为了提高 BN 层的表达能力，BN 层作者引入了“scale and shift”技巧，将x^变量再次映射变换：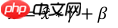 
其中γ参数实现对标准化后的x^再次进行缩放，β参数实现对标准化的x^进行平移。不同的是，γ 、β参数均由反向传播算法自动优化，实现网络层“按需”缩放平移数据的分布的目的。 于是，在测试阶段，标准化公式与缩放平移结合变为：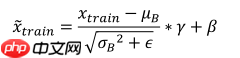
六、Dropout
比较经典的几个神经网络：
一、LeNet
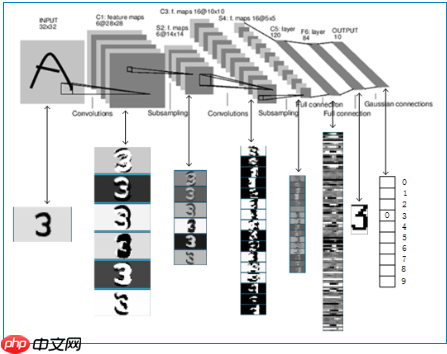
LeNet-5是一个较简单的卷积神经网络。下图显示了其结构：输入的二维图像，先经过两次卷积层到池化层，再经过全连接层，最后使用softmax分类作为输出层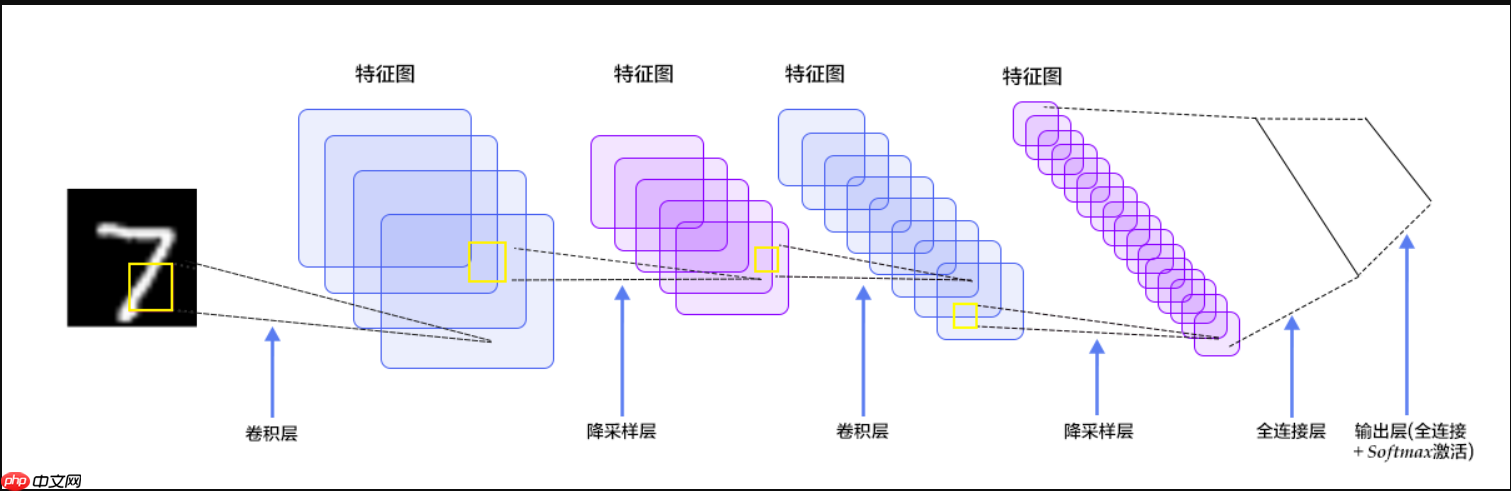
LeNet-5 这个网络虽然很小，但是它包含了深度学习的基本模块：卷积层，池化层，全连接层。是其他深度学习模型的基础， 这里我们对LeNet-5进行深入分析。同时，通过实例分析，加深对与卷积层和池化层的理解。
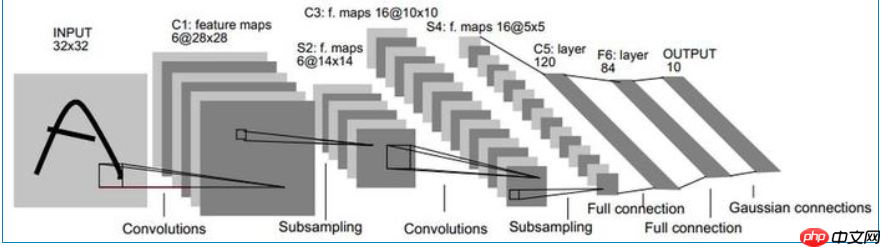LeNet-5共有7层，不包含输入，每层都包含可训练参数；每个层有多个Feature Map，每个FeatureMap通过一种卷积滤波器提取输入的一种特征，然后每个FeatureMap有多个神经元。
各层参数详解：
1. INPUT层-输入层
首先是数据 INPUT 层，输入图像的尺寸统一归一化为32*32。
注意：本层不算LeNet-5的网络结构，传统上，不将输入层视为网络层次结构之一。
2. C1层-卷积层
输入图片：32*32
卷积核大小：5*5
卷积核种类：6
输出featuremap大小：28*28 （32-5+1）=28
神经元数量：28286
可训练参数：（55+1) * 6（每个滤波器55=25个unit参数和一个bias参数，一共6个滤波器）
连接数：（55+1）62828=122304
详细说明：对输入图像进行第一次卷积运算（使用 6 个大小为 55 的卷积核），得到6个C1特征图（6个大小为2828的 feature maps, 32-5+1=28）。我们再来看看需要多少个参数，卷积核的大小为55，总共就有6（55+1）=156个参数，其中+1是表示一个核有一个bias。对于卷积层C1，C1内的每个像素都与输入图像中的55个像素和1个bias有连接，所以总共有1562828=122304个连接（connection）。有122304个连接，但是我们只需要学习156个参数，主要是通过权值共享实现的。
3. S2层-池化层（下采样层）
输入：28*28
采样区域：2*2
采样方式：4个输入相加，乘以一个可训练参数，再加上一个可训练偏置。结果通过sigmoid
采样种类：6
输出featureMap大小：14*14（28/2）
神经元数量：14146
可训练参数：2*6（和的权+偏置）
连接数：（22+1）61414
S2中每个特征图的大小是C1中特征图大小的1/4。
详细说明：第一次卷积之后紧接着就是池化运算，使用 22核 进行池化，于是得到了S2，6个1414的 特征图（28/2=14）。S2这个pooling层是对C1中的2*2区域内的像素求和乘以一个权值系数再加上一个偏置，然后将这个结果再做一次映射。于是每个池化核有两个训练参数，所以共有2x6=12个训练参数，但是有5x14x14x6=5880个连接。
4. C3层-卷积层
输入：S2中所有6个或者几个特征map组合
卷积核大小：5*5
卷积核种类：16
输出featureMap大小：10*10 (14-5+1)=10
C3中的每个特征map是连接到S2中的所有6个或者几个特征map的，表示本层的特征map是上一层提取到的特征map的不同组合。
存在的一个方式是：C3的前6个特征图以S2中3个相邻的特征图子集为输入。接下来6个特征图以S2中4个相邻特征图子集为输入。然后的3个以不相邻的4个特征图子集为输入。最后一个将S2中所有特征图为输入。则：可训练参数：6*(355+1)+6*(455+1)+3*(455+1)+1*(655+1)=1516
连接数：10101516=151600
详细说明：第一次池化之后是第二次卷积，第二次卷积的输出是C3，16个10x10的特征图，卷积核大小是 55. 我们知道S2 有6个 1414 的特征图，怎么从6 个特征图得到 16个特征图了？ 这里是通过对S2 的特征图特殊组合计算得到的16个特征图。具体如下：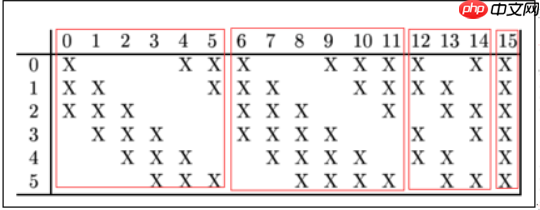 
C3的前6个feature map（对应上图第一个红框的6列）与S2层相连的3个feature map相连接（上图第一个红框），后面6个feature map与S2层相连的4个feature map相连接（上图第二个红框），后面3个feature map与S2层部分不相连的4个feature map相连接，最后一个与S2层的所有feature map相连。卷积核大小依然为55，所以总共有6(355+1)+6*(455+1)+3*(455+1)+1*(655+1)=1516个参数。而图像大小为10*10，所以共有151600个连接。
C3与S2中前3个图相连的卷积结构如下图所示：
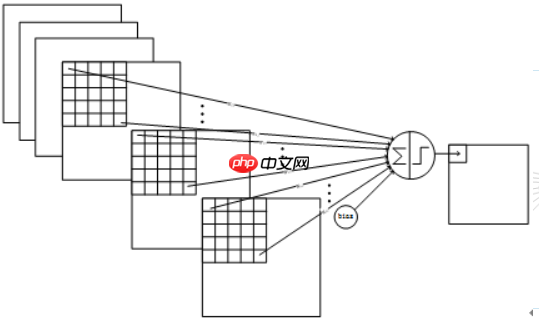
上图对应的参数为 355+1，一共进行6次卷积得到6个特征图，所以有6*（355+1）参数。 为什么采用上述这样的组合了？论文中说有两个原因：1）减少参数，2）这种不对称的组合连接的方式有利于提取多种组合特征。
5. S4层-池化层（下采样层）
输入：10*10
采样区域：2*2
采样方式：4个输入相加，乘以一个可训练参数，再加上一个可训练偏置。结果通过sigmoid
采样种类：16
输出featureMap大小：5*5（10/2）
神经元数量：5516=400
可训练参数：2*16=32（和的权+偏置）
连接数：16*（2*2+1）55=2000
S4中每个特征图的大小是C3中特征图大小的1/4
详细说明：S4是pooling层，窗口大小仍然是2*2，共计16个feature map，C3层的16个10x10的图分别进行以2x2为单位的池化得到16个5x5的特征图。这一层有2x16共32个训练参数，5x5x5x16=2000个连接。连接的方式与S2层类似。
6. C5层-卷积层
输入：S4层的全部16个单元特征map（与s4全相连）
卷积核大小：5*5
卷积核种类：120
输出featureMap大小：1*1（5-5+1）
可训练参数/连接：120*（1655+1）=48120
详细说明：C5层是一个卷积层。由于S4层的16个图的大小为5x5，与卷积核的大小相同，所以卷积后形成的图的大小为1x1。这里形成120个卷积结果。每个都与上一层的16个图相连。所以共有(5x5x16+1)x120 = 48120个参数，同样有48120个连接。C5层的网络结构如下：
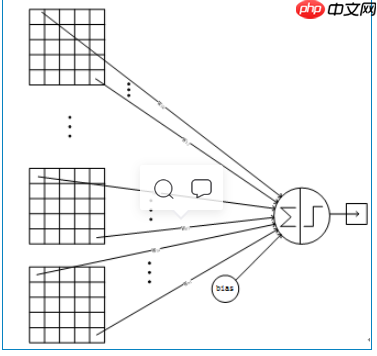
7. F6层-全连接层
输入：c5 120维向量
计算方式：计算输入向量和权重向量之间的点积，再加上一个偏置，结果通过sigmoid函数输出。
可训练参数:84*(120+1)=10164
详细说明：6层是全连接层。F6层有84个节点，对应于一个7x12的比特图，-1表示白色，1表示黑色，这样每个符号的比特图的黑白色就对应于一个编码。该层的训练参数和连接数是(120 + 1)x84=10164。 F6层的连接方式如下：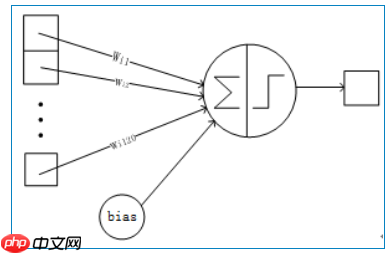
8. Output层-全连接层
Output层也是全连接层，共有10个节点，分别代表数字0到9，且如果节点i的值为0，则网络识别的结果是数字i。采用的是径向基函数（RBF）的网络连接方式。假设x是上一层的输入，y是RBF的输出，则RBF输出的计算方式是：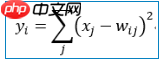
网络解析（一）：LeNet-5详解
上式w_ij 的值由i的比特图编码确定，i从0到9，j取值从0到7*12-1。RBF输出的值越接近于0，则越接近于i，即越接近于i的ASCII编码图，表示当前网络输入的识别结果是字符i。该层有84x10=840个参数和连接。
总结： LeNet-5是一种用于手写体字符识别的非常高效的卷积神经网络。 卷积神经网络能够很好的利用图像的结构信息。 卷积层的参数较少，这也是由卷积层的主要特性即局部连接和共享权重所决定。
9.代码实现
# LeNetimport paddleimport paddle.nn.functional as F#定义模型class LeNetModel(paddle.nn.Layer):
def __init__(self):
super(LeNetModel, self).__init__() # 创建卷积和池化层块，每个卷积层后面接着2x2的池化层
#卷积层L1
self.conv1 = paddle.nn.Conv2D(in_channels=1,
out_channels=6,
kernel_size=5,
stride=1) #池化层L2
self.pool1 = paddle.nn.MaxPool2D(kernel_size=2,
stride=2) #卷积层L3
self.conv2 = paddle.nn.Conv2D(in_channels=6,
out_channels=16,
kernel_size=5,
stride=1) #池化层L4
self.pool2 = paddle.nn.MaxPool2D(kernel_size=2,
stride=2) #线性层L5
self.fc1=paddle.nn.Linear(256,120) #线性层L6
self.fc2=paddle.nn.Linear(120,84) #线性层L7
self.fc3=paddle.nn.Linear(84,10) #正向传播过程
def forward(self, x):
x = self.conv1(x)
x = F.relu(x)
x = self.pool1(x)
x = F.relu(x)
x = self.conv2(x)
x = self.pool2(x)
x = paddle.flatten(x, start_axis=1,stop_axis=-1)
x = self.fc1(x)
x = F.relu(x)
x = self.fc2(x)
x = F.relu(x)
out = self.fc3(x) return out
data = paddle.randn([1,1,28,28])print(data.shape)
net = LeNetModel()
predict = net(data)print(predict.shape)
[1, 1, 28, 28] [1, 10]
二、AlexNet
1. AlexNet的概述
AlexNet由Geoffrey和他的学生Alex提出，并在2012年的ILSVRC竞赛中获得了第一名。Alexnet共有8层结构，前5层为卷积层，后三层为全连接层。
AlexNet网络结构具有如下特点：
1.1 AlexNet在激活函数上选取了非线性非饱和的relu函数，在训练阶段梯度衰减快慢方面，relu函数比传统神经网络所选取的非线性饱和函数（如sigmoid函数，tanh函数）要快许多。
1.2 AlexNet在双gpu上运行，每个gpu负责一半网络的运算
1.3 采用局部响应归一化（LRN）。对于非饱和函数relu来说，不需要对其输入进行标准化，但Alex等人发现，在relu层加入LRN，可形成某种形式的横向抑制，从而提高网络的泛华能力。
1.4 池化方式采用overlapping pooling。即池化窗口的大小大于步长，使得每次池化都有重叠的部分。（ps:这种重叠的池化方式比传统无重叠的池化方式有着更好的效果，且可以避免过拟合现象的发生）
2. AlexNet网络结构
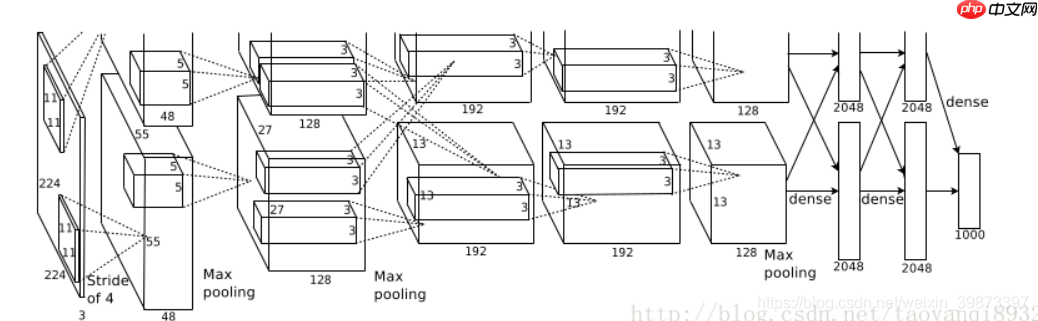第一个卷积层
输入的图片大小为:2242243，为后续处理方便，普遍改为2272273
第一个卷积层为:11113即卷积核尺寸为1111,有96个卷积核,步长为4,卷积层后跟ReLU,因此输出的尺寸为 （227-11）/4+1=55,因此其输出的每个特征图 为 5555*96,同时后面经过LRN层处理,尺寸不变.
最大池化层,池化核大小为33,步长为2,输出的尺寸为 （55-3）/2+1=27，因此特征图的大小为:272796。由于双gpu处理，故每组数据有2727*48个特征图，共两组数据，分别在两个gpu中进行运算
第二层卷积层
每组输入的数据为272748，共两组数据
每组数据都被128个卷积核大小为: 5548进行卷积运算,步长为1,尺寸不会改变,同样紧跟ReLU,和LRN层进行处理.
最大池化层,核大小为33,步长为2,因此输出两组特征图:1313*128
第三层至第五层卷积层
输入的数据为1313128，共两组
第三层每组数据都被尺寸为 33192的卷积核进行卷积运算,步长为1,加上ReLU，得到两组1313192的像素层
第四层经过padding=1填充后，每组数据都被尺寸大小为 33192的卷积核卷积运算,步长为1,加上ReLU，输出两组1313192的像素层
第五层经过padding=1填充后，每组数据都被尺寸大小为 33128的卷积核进行卷积运算,步长为1,加上ReLU，输出两组1313128的像素层
经过33池化窗口，步长为2，池化后输出两组66*256的像素层
第六层至第八层全连接层
接下来的三层为全连接层,分别为:
6层. 4096 个神经元+ ReLU
7层. 4096个神经元 + ReLU
8层. 1000 个神经元，最后一层为softmax为1000类的概率值.
3.代码实现
# AlexNetimport paddleimport paddle.nn.functional as Fimport numpy as npclass AlexNetModel(paddle.nn.Layer):
def __init__(self):
super(AlexNetModel, self).__init__()
self.conv_pool1 = paddle.nn.Sequential( #输入大小m*3*227*227
paddle.nn.Conv2D(3,96,11,4,0), #L1, 输出大小m*96*55*55
paddle.nn.ReLU(), #L2, 输出大小m*96*55*55
paddle.nn.MaxPool2D(kernel_size=3, stride=2)) #L3, 输出大小m*96*27*27
self.conv_pool2 = paddle.nn.Sequential(
paddle.nn.Conv2D(96, 256, 5, 1, 2), #L4, 输出大小m*256*27*27
paddle.nn.ReLU(), #L5, 输出大小m*256*27*27
paddle.nn.MaxPool2D(3, 2)) #L6, 输出大小m*256*13*13
self.conv_pool3 = paddle.nn.Sequential(
paddle.nn.Conv2D(256, 384, 3, 1, 1),#L7, 输出大小m*384*13*13
paddle.nn.ReLU()) #L8, 输出m*384*13*13
self.conv_pool4 = paddle.nn.Sequential(
paddle.nn.Conv2D(384, 384, 3, 1, 1),#L9, 输出大小m*384*13*13
paddle.nn.ReLU()) #L10, 输出大小m*384*13*13
self.conv_pool5 = paddle.nn.Sequential(
paddle.nn.Conv2D(384, 256, 3, 1, 1),#L11, 输出大小m*256*13*13
paddle.nn.ReLU(), #L12, 输出大小m*256*13*13
paddle.nn.MaxPool2D(3, 2)) #L13, 输出大小m*256*6*6
self.full_conn = paddle.nn.Sequential(
paddle.nn.Linear(256*6*6, 4096), #L14, 输出大小m*4096
paddle.nn.ReLU(), #L15, 输出大小m*4096
paddle.nn.Dropout(0.5), #L16, 输出大小m*4096
paddle.nn.Linear(4096, 4096), #L17, 输出大小m*4096
paddle.nn.ReLU(), #L18, 输出大小m*4096
paddle.nn.Dropout(0.5), #L19, 输出大小m*4096
paddle.nn.Linear(4096, 10)) #L20, 输出大小m*10
self.flatten=paddle.nn.Flatten() def forward(self, x): #前向传播
x = self.conv_pool1(x)
x = self.conv_pool2(x)
x = self.conv_pool3(x)
x = self.conv_pool4(x)
x = self.conv_pool5(x)
x = self.flatten(x)
x = self.full_conn(x) return x
data = paddle.randn([1,3,227,227])print(data.shape)
net = AlexNetModel()
predict = net(data)print(predict.shape)
[1, 3, 227, 227] [1, 10]
三、残差神经网络（ResNet）
残差神经网络(ResNet)是由微软研究院的何恺明、张祥雨、任少卿、孙剑等人提出的。ResNet 在2015 年的ILSVRC（ImageNet Large Scale Visual Recognition Challenge）中取得了冠军。
残差神经网络的主要贡献是发现了“退化现象（Degradation）”，并针对退化现象发明了 “快捷连接（Shortcut connection）”，极大的消除了深度过大的神经网络训练困难问题。神经网络的“深度”首次突破了100层、最大的神经网络甚至超过了1000层。
1. 从一个信念说起
在2012年的ILSVRC挑战赛中，AlexNet取得了冠军，并且大幅度领先于第二名。由此引发了对AlexNet广泛研究，并让大家树立了一个信念——“越深网络准确率越高”。这个信念随着VGGNet、Inception v1、Inception v2、Inception v3不断验证、不断强化，得到越来越多的认可，但是，始终有一个问题无法回避，这个信念正确吗？
它是正确的，至少在理论上是正确的。
假设一个层数较少的神经网络已经达到了较高准确率，我们可以在这个神经网络之后，拼接一段恒等变换的网络层，这些恒等变换的网络层对输入数据不做任何转换，直接返回（y=x），就能得到一个深度较大的神经网络，并且，这个深度较大的神经网络的准确率等于拼接之前的神经网络准确率，准确率没有理由降低。
2. 退化现象与对策
通过实验，ResNet随着网络层不断的加深，模型的准确率先是不断的提高，达到最大值（准确率饱和），然后随着网络深度的继续增加，模型准确率毫无征兆的出现大幅度的降低。
这个现象与“越深的网络准确率越高”的信念显然是矛盾的、冲突的。ResNet团队把这一现象称为“退化（Degradation）”。
ResNet团队把退化现象归因为深层神经网络难以实现“恒等变换（y=x）”。乍一看，让人难以置信，原来能够模拟任何函数的深层神经网络，竟然无法实现恒等变换这么简单的映射了？
让我们来回想深度学习的起源，与传统的机器学习相比，深度学习的关键特征在于网络层数更深、非线性转换（激活）、自动的特征提取和特征转换，其中，非线性转换是关键目标，它将数据映射到高纬空间以便于更好的完成“数据分类”。随着网络深度的不断增大，所引入的激活函数也越来越多，数据被映射到更加离散的空间，此时已经难以让数据回到原点（恒等变换）。或者说，神经网络将这些数据映射回原点所需要的计算量，已经远远超过我们所能承受的。
退化现象让我们对非线性转换进行反思，非线性转换极大的提高了数据分类能力，但是，随着网络的深度不断的加大，我们在非线性转换方面已经走的太远，竟然无法实现线性转换。显然，在神经网络中增加线性转换分支成为很好的选择，于是，ResNet团队在ResNet模块中增加了快捷连接分支，在线性转换和非线性转换之间寻求一个平衡。
3. ResNet网络架构
按照这个思路，ResNet团队分别构建了带有“快捷连接（Shortcut Connection）”的ResNet构建块、以及降采样的ResNet构建块，区降采样构建块的主杆分支上增加了一个1×1的卷积操作，见图2。
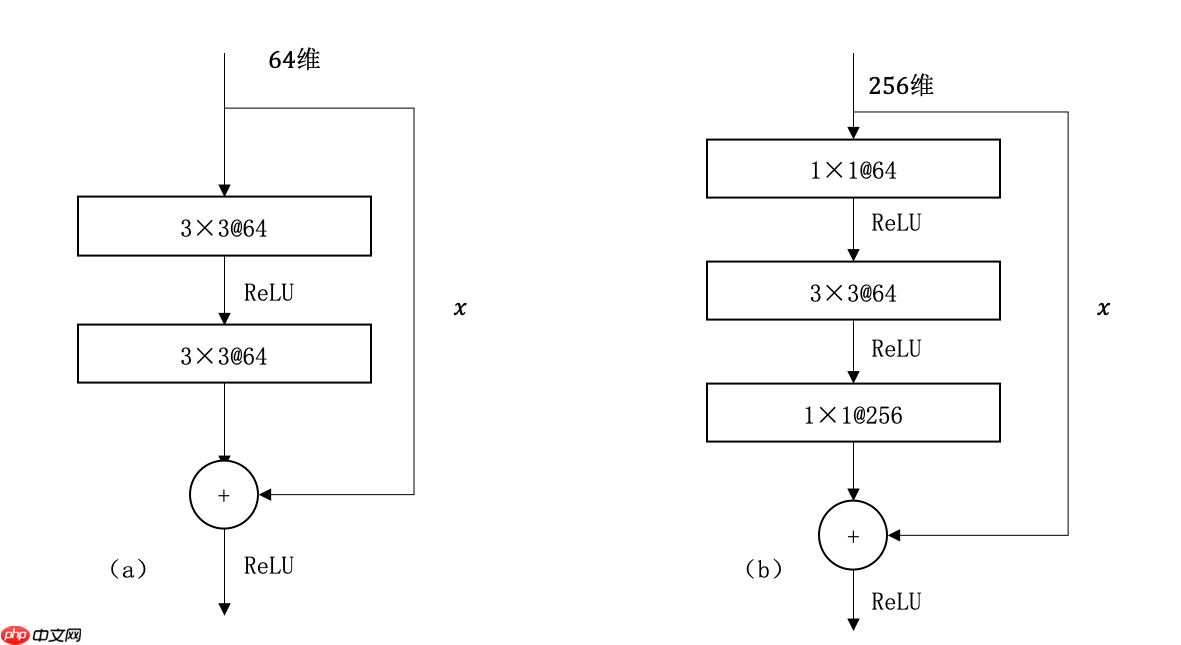
图2 ResNet构建块示意图
图3展示了34层ResNet模型的架构图，仿照AlexNet的8层网络结构，我们也将ResNet划分成8个构建层（Building Layer）。一个构建层可以包含一个或多个网络层、以及一个或多个构建块（如ResNet构建块）。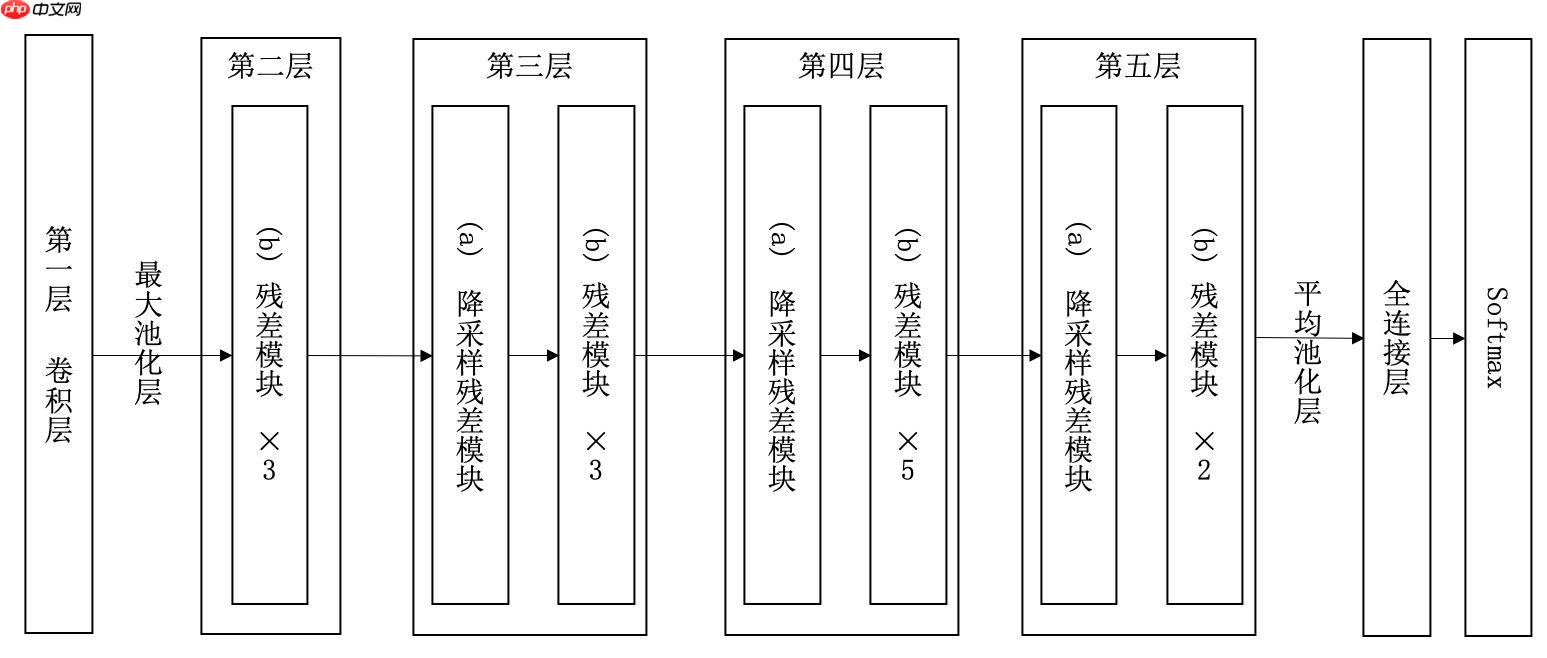
第一个构建层，由1个普通卷积层和最大池化层构建。
第二个构建层，由3个残差模块构成。
第三、第四、第五构建层，都是由降采样残差模块开始，紧接着3个、5个、2个残差模块。
其余各个构建层见图3。
4. 代码实现
# resnetimport paddleimport paddle.nn.functional as Fimport numpy as np#构建模型class Residual(paddle.nn.Layer):
def __init__(self, in_channel, out_channel, use_conv1x1=False, stride=1):
super(Residual, self).__init__()
self.conv1 = paddle.nn.Conv2D(in_channel, out_channel, kernel_size=3, padding=1, stride=stride)
self.conv2 = paddle.nn.Conv2D(out_channel, out_channel, kernel_size=3, padding=1) if use_conv1x1: #使用1x1卷积核
self.conv3 = paddle.nn.Conv2D(in_channel, out_channel, kernel_size=1, stride=stride) else:
self.conv3 = None
self.batchNorm1 = paddle.nn.BatchNorm2D(out_channel)
self.batchNorm2 = paddle.nn.BatchNorm2D(out_channel) def forward(self, x):
y = F.relu(self.batchNorm1(self.conv1(x)))
y = self.batchNorm2(self.conv2(y)) if self.conv3:
x = self.conv3(x)
out = F.relu(y+x) #核心代码
return outdef ResNetBlock(in_channel, out_channel, num_layers, is_first=False):
if is_first: assert in_channel == out_channel
block_list = [] for i in range(num_layers): if i == 0 and not is_first:
block_list.append(Residual(in_channel, out_channel, use_conv1x1=True, stride=2)) else:
block_list.append(Residual(out_channel, out_channel))
resNetBlock = paddle.nn.Sequential(*block_list) #用*号可以把list列表展开为元素
return resNetBlockclass ResNetModel(paddle.nn.Layer):
def __init__(self):
super(ResNetModel, self).__init__()
self.b1 = paddle.nn.Sequential(
paddle.nn.Conv2D(3, 64, kernel_size=7, stride=2, padding=3),
paddle.nn.BatchNorm2D(64),
paddle.nn.ReLU(),
paddle.nn.MaxPool2D(kernel_size=3, stride=2, padding=1))
self.b2 = ResNetBlock(64, 64, 2, is_first=True)
self.b3 = ResNetBlock(64, 128, 2)
self.b4 = ResNetBlock(128, 256, 2)
self.b5 = ResNetBlock(256, 512, 2)
self.AvgPool = paddle.nn.AvgPool2D(2)
self.flatten = paddle.nn.Flatten()
self.Linear = paddle.nn.Linear(512, 10)
def forward(self, x):
x = self.b1(x)
x = self.b2(x)
x = self.b3(x)
x = self.b4(x)
x = self.b5(x)
x = self.AvgPool(x)
x = self.flatten(x)
x = self.Linear(x) return x
data = paddle.randn([1,3,96,96])print(data.shape)
net = ResNetModel()
predict = net(data)print(predict.shape)
[1, 3, 96, 96] [1, 10]
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/paddle/nn/layer/norm.py:654: UserWarning: When training, we now always track global mean and variance. "When training, we now always track global mean and variance.")
CNN改进思路
一、优化指标
1.准确率
2.速度
3.内存消耗
不同的网络（如VGG、Inception 以及 ResNet 等）在这些指标上有不同的权衡。此外，你还可以修改这些网络结构，例如通过削减某些层、增加某些层、在网络内部使用扩张卷积，或者不同的网络训练技巧。 关于Inception 以及 ResNet等内容可参考 #[ 博客链接 ]
结论:看重准确率，用超深层的 ResNet；看重速度，用 Inception。
二、 优化CNN的通用型方法：
1.从数据角度出发
数据清洗、数据增强
同时针对class skew（数据偏斜/数据不均衡）的情况，可以采取以下方法：
(1).过采样：
针对数据很小的情况，对训练样本中数量不足的类别进行重复采样，这样有助于样本分布的均衡化。当可用数据较少的时候这个方法最能奏效。
(2).降采样：
针对数据量很大的情况，对数据先进行聚类，再将大的簇进行随机欠采样或者小的簇进行数据生成
(3).SMOTE算法：
对数据进行采用的过程中通过相似性同时生成并插样“少数类别数据”
(4).集成学习：
先对多数类别进行随机的欠采样，并结合boosting算法进行集成学习
(5).类别权重：
损失函数中使用类别权重：样本不足的类别赋予更高权重
(6).改变学习方法：
把监督学习变为无监督学习，舍弃掉标签把问题转化为一个无监督问题，如异常检测
2.从卷积设计出发
以下列举一些能够在没有太多的准确率损失的情况下加速 CNN 的运行，并减少内存消耗的方法。注意：所有方法都可以很容易地应用到任何一类CNN（卷积神经网络）的设计中。
MobileNets论文
使用深度分离的卷积来极大地减少运算和内存的消耗，同时仅牺牲 1% 到 5% 的准确率，准确率的牺牲程度取决于你想要获得的计算节约。
XNOR-Net论文
使用二进制卷积，意味着，卷积运算只涉及两个可能的数值：0 或者 1。通过这种设计，网络可以具有较高程度的稀疏性，易于被压缩而不消耗太多内存。
ShuffleNet论文
使用点组卷积和通道随机化来极大地减少计算代价，同时还能维持比 MobileNets 高的准确率。事实上，它们可以在超过 10 倍的运算速度下达到早期最先进的分类 CNN 的准确率。
Network Pruning论文
删除 CNN 的部分权重的技术，而且有希望不降低准确率。为了保持准确率，被删除的部分应该对最终结果没有大的影响。链接中的论文展示了使用 ResNets 可以轻易地做到这一点。
3. 卷积核
通常来说，更大的卷积核准确率越高，但训练速度会变慢消耗内存也会更多，并且较大的卷积核会导致网络泛化能力很差，ResNet 和VGGNet 都相当全面的诠释了这一点
DilatedConvolution（扩张卷积）
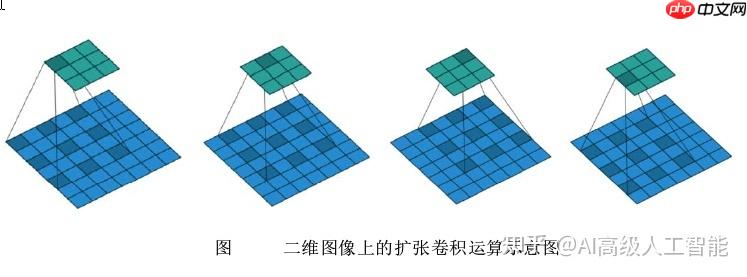
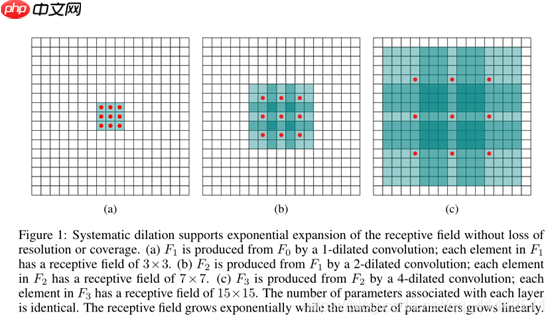
上图中(a)是基础的卷积核，扩张卷积就是在这个基础卷积核加入间隔，上图(b)对应3 × 3 的dilation rate=2的卷积，但是间隔为1，也就是相当于对应7 × 7的图像块，可以理解为kernel size还是变成了7 × 7 ，但是却只有9个点有参数，其余的位置参数都是0，和输入特征图对应位置的像素进行卷积计算，其余的位置都略过。图©和图(b)是类似的，只是dilation rate=4，相当于变成了15 × 15 的卷积核。 而卷积核尺寸变大了，感受野也就自然变大。
4. 网络规模（宽度/深度）
宽度使得每一层学习到更加丰富的特征，以人脸识别为例，可以学到不同方向，不同频率的纹理特征，对于一个模型来说，浅层的特征非常重要，因此网络浅层的宽度是一个非常敏感的系数。宽度带来的计算量是平方级增长的。同时宽度带来的好处受制于边际效应，增加的每层的宽度越大，通过增加层宽而带来的模型性能提升也会越少。
网络更深带来的一个非常大的好处，就是逐层的抽象，不断精炼提取知识，如第一层学习到了边缘，第二层学习到了简单的形状，第三层开始学习到了目标的形状，更深的网络层能学习到更加复杂的表达。
选择合适的网络深度也是设计的重要思想之一，通常增加更多地层会提升准确率，同时会牺牲一些速度和内存。但是受制于边际效应，增加的层越多，通过增加每一层而带来的准确率提升将越少。
5. 激活函数选取
通常使用 ReLU 会在开始的时立即得到一些好的结果，但如果当ReLU得不到好的结果的适合，可以换成Sigmoid函数，如果还是不行则调整模型其它的部分，以尝试对准确率做提升。都得不到好结果的情况下，可以试着使用ELU、PReLU 、Sigmoid或者LeakyReLU等激活函数。
6.举列子
Oxford flower 102 数据集+ResNet
ResNetV1的残差结构：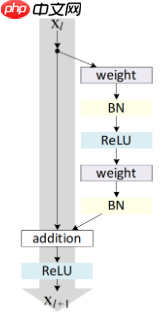
ResNetV2的残差结构：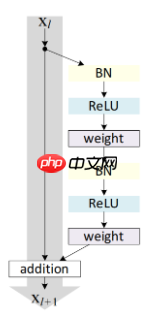
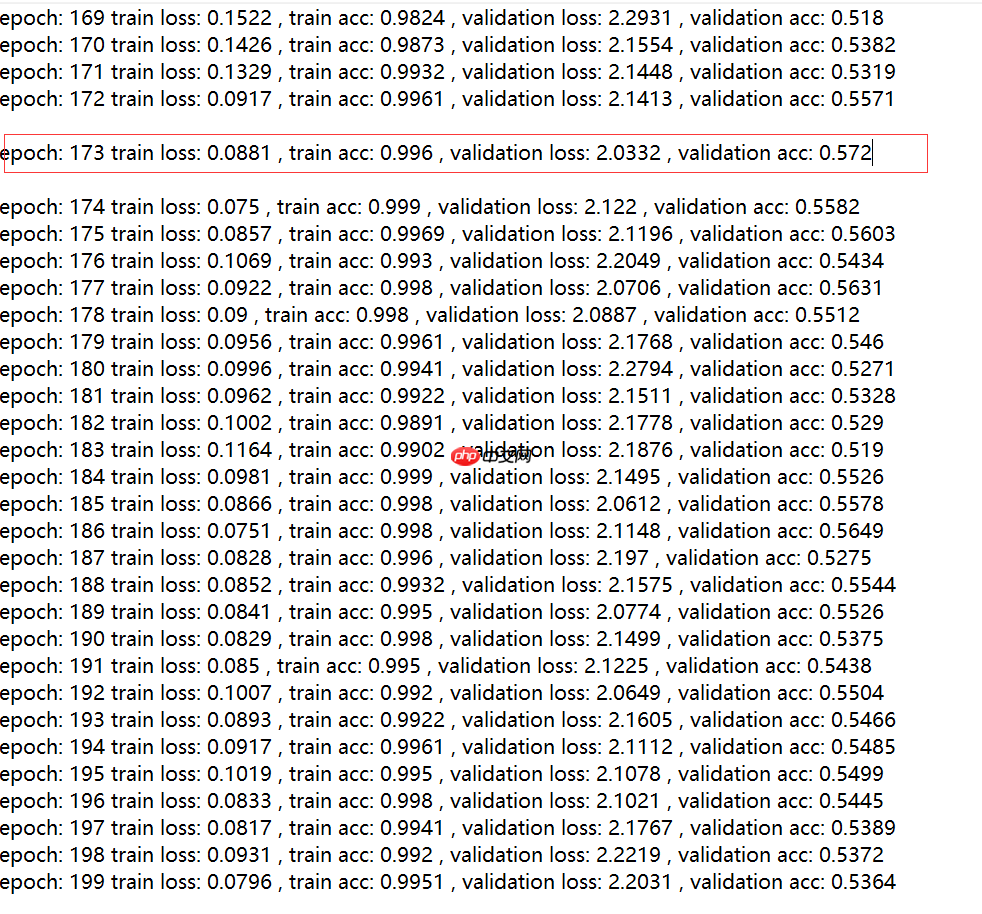
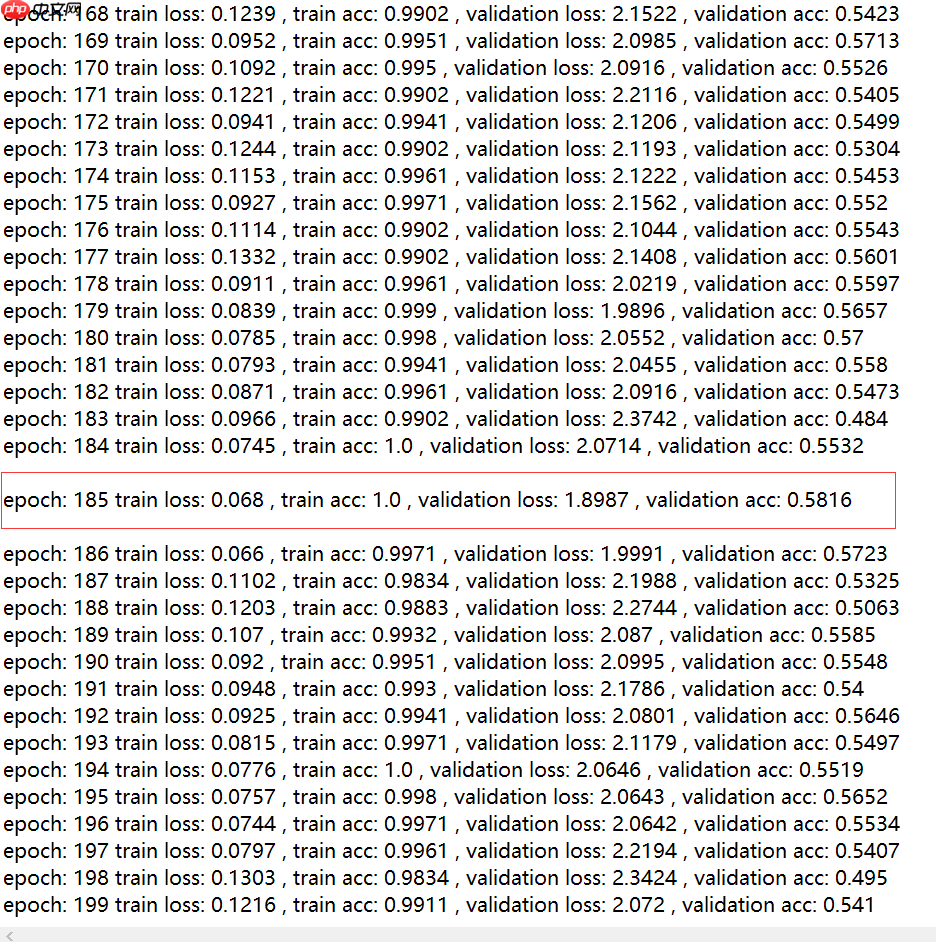
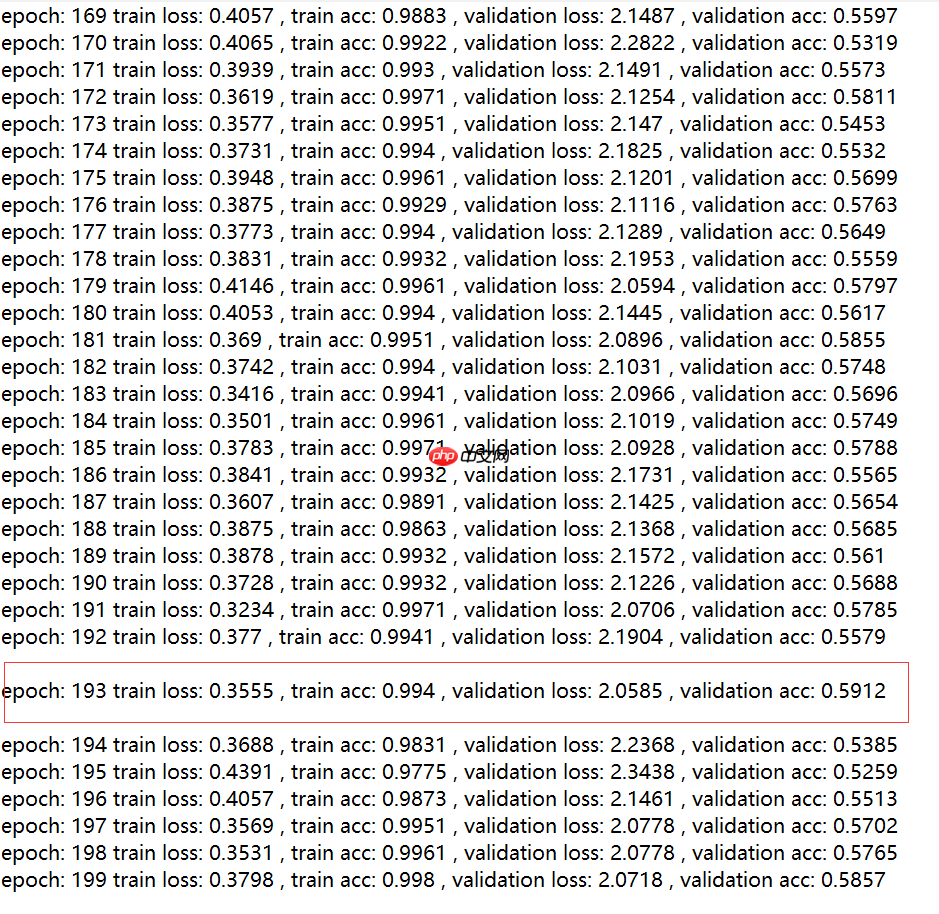
这里我做了四组实验：这里除了改了激活函数和残差块的结构其他均保持相同
(1).ResNetV1+relu
(2).ResNetV1+leaky_relu(将relu替换为leaky_relu)
(3).ResNetV2+relu
(4).ResNetV2+leaky_relu(将relu替换为leaky_relu)
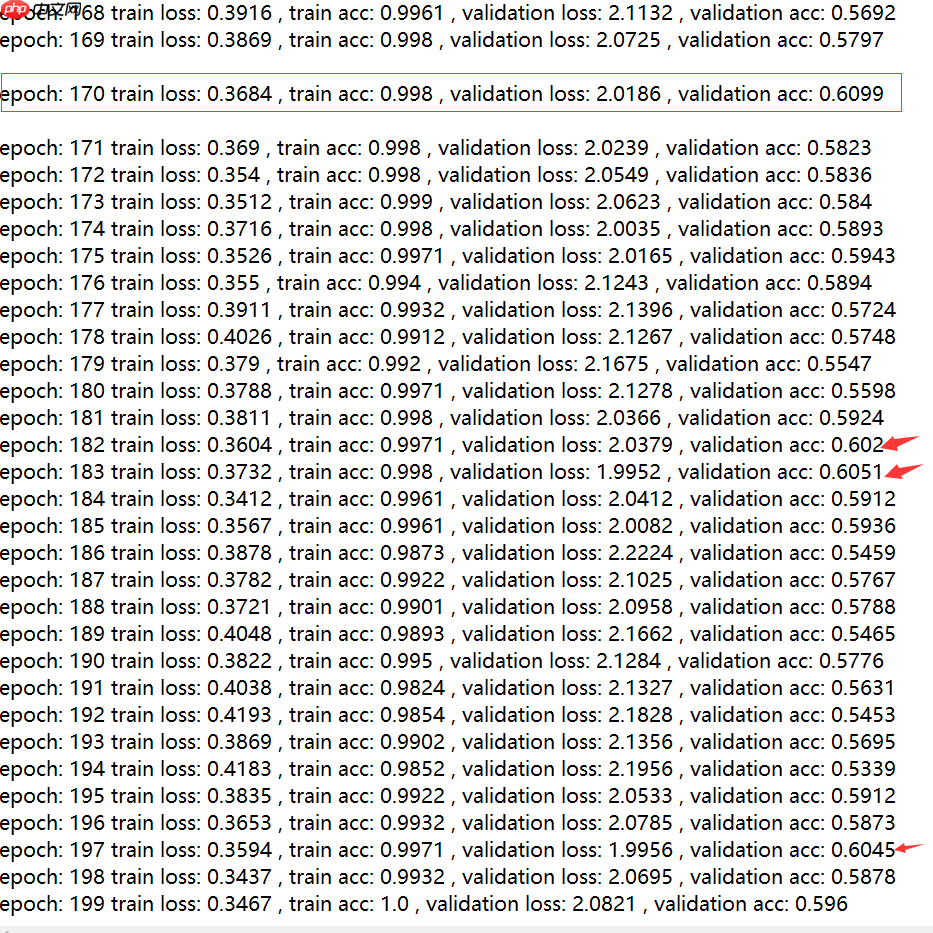
从结果可以看出：v2比v1好，改用leaky_relu激活函数比relu激活函数要好。
