不要改变原内容的意思，微调内容，重写内容，不要续写。“分位数回归满足这一需求，提供具有量化机会的预测区间。它是一种统计技术，用于模拟预测变量与响应变量之间的关系，特别是当响应变量的条件分布命令人感兴趣时。与传统的回归方法不同，分位数回归侧重于估计响应变量变量的条件量值，而不是条件均值。”
☞☞☞AI 智能聊天, 问答助手, AI 智能搜索, 免费无限量使用 DeepSeek R1 模型☜☜☜
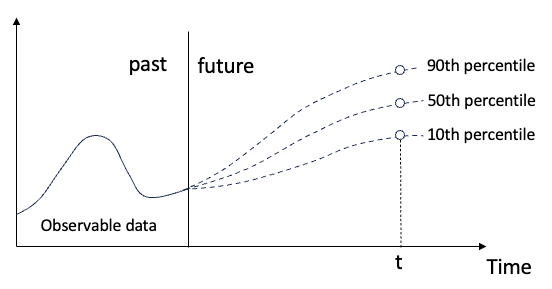图(A): 分位数回归
分位数回归概念
分位数回归是估计⼀组回归变量X与被解释变量Y的分位数之间线性关系的建模⽅法。
现有的回归模型实际上是研究被解释变量与解释变量之间关系的一种方法。他们关注解释变量与被解释变量之间的关系及其误差分布的情况，其中位数回归和分位数回归是两种常见的回归模型。它们是根据Koenker和Bassett (1978) 首次提出的。
普通最小二乘回归估计量的计算基于最小化残差平方和。分位数回归估计量的计算也是基于种对称形式的绝对值残差最小化。其中，中位数回归运算的是最绝对值差估计（LAD，least absolute deviations estimator）。
分位数回归的优点
解释被解释变量条件分布的全貌，并不只是分析被解释变量的条件期望（均值），也可分析解释变量如何影响被解释变量的中位数、分位数等。不同分位数下的回归系数估计常常不同，即解释变量对不同分位数的影响效果不同，因此解释变量不同分位数的影响不同会对被解释变量的影响产生不同。
进行中位数回归的估计法与最小乘法相比，估计结果对离群值则表现的更加稳健，且分位数回归对误差项并不要求很强的假设条件，因此对于非正态状态下的分布，中位数回归系数量则更加健康。同时，分位数回归系统量估计则加稳健。
分位数回归相对于蒙特卡罗模拟具有哪些优势呢？首先，分位数回归直接估计给定预测因子的响应变量的条件量值。这意味着，它不像蒙特卡罗模拟那样产生大量可能的结果，而是提供了响应变量分布的特定量级的估计值。这对于了解不同层次的预测不确定性特别有用，例如二分位数、四分位数或极端量值。其次，分位数回归提供了一种基于模型的预测不确定性估算方法，利用观测数据来估计变量之间的关系，并根据这种关系进行预测。相比之下，蒙特卡罗模拟依赖于为输入变量指定概率分布，并根据随机抽样生成结果。
NeuralProphet提供两种统计技术：（1）分位数回归和（2）保形分位数回归。共形分位数预测技术增加了一个校准过程来做分位数回归。在本文中，我们将使用Neural Prophet的分位数回归模块来做分位数回归预测。这个模块增加了一个校准过程，来保证预测结果与观测数据的分布一致。我们将在本章中使用Neural Prophet的分位数回归模块。
环境要求
安装 NeuralProphet。
!pip install neuralprophet!pip uninstall numpy!pip install git+https://github.com/ourownstory/neural_prophet.git numpy==1.23.5
导入需要的库。
%matplotlib inlinefrom matplotlib import pyplot as pltimport pandas as pdimport numpy as npimport loggingimport warningslogging.getLogger('prophet').setLevel(logging.ERROR)warnings.filterwarnings("ignore")数据集
共享单车数据。该数据集是一个多变量数据集，包含每日租赁需求以及温度或风速等其他天气领域。
data = pd.read_csv('/bike_sharing_daily.csv')data.tail()
图(B): 共享单车
绘制共享单车的数量图。我们观察到，需求量在第二年有所增加，而且有季节性规律。
# convert string to datetime64data["ds"] = pd.to_datetime(data["dteday"])# create line plot of sales dataplt.plot(data['ds'], data["cnt"])plt.xlabel("date")plt.ylabel("Count")plt.show()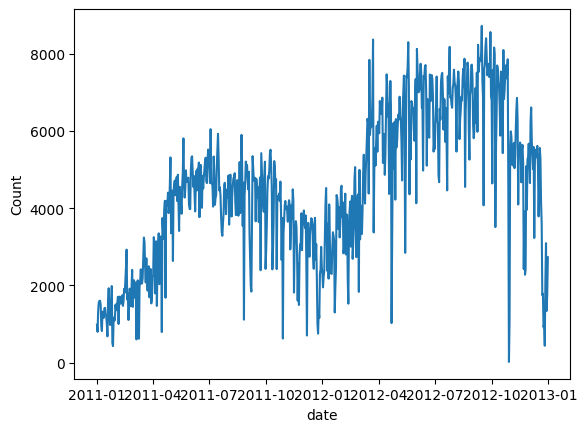
图 (C)：自行车租赁日需求量
为建模做最基本的数据准备。NeuralProphet 要求列名为 ds 和 y，这与 Prophet 的要求相同。
df = data[['ds','cnt']]df.columns = ['ds','y']
构建分位数回归模型
直接在 NeuralProphet 中构建分位数回归。假设我们需要第 5、10、50、90 和 95 个量级的值。我们指定 quantile_list = [0.05,0.1,0.5,0.9,0.95]，并打开参数 quantiles = quantile_list。
from neuralprophet import NeuralProphet, set_log_levelquantile_list=[0.05,0.1,0.5,0.9,0.95 ]# Model and predictionm = NeuralProphet(quantiles=quantile_list,yearly_seasnotallow=True,weekly_seasnotallow=True,daily_seasnotallow=False)m = m.add_country_holidays("US")m.set_plotting_backend("matplotlib")# Use matplotlibdf_train, df_test = m.split_df(df, valid_p=0.2)metrics = m.fit(df_train, validation_df=df_test, progress="bar")metrics.tail()分位数回归预测
我们将使用 .make_future_dataframe()为预测创建新数据帧，NeuralProphet 是基于 Prophet 的。参数 n_historic_predictions 为 100，只包含过去的 100 个数据点。如果设置为 True，则包括整个历史数据。我们设置 period=50 来预测未来 50 个数据点。
future = m.make_future_dataframe(df, periods=50, n_historic_predictinotallow=100) #, n_historic_predictinotallow=1)# Perform prediction with the trained modelsforecast = m.predict(df=future)forecast.tail(60)
预测结果存储在数据框架 predict 中。
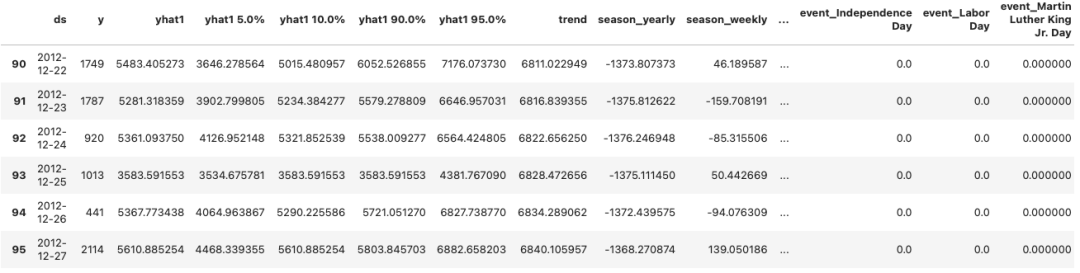图 (D)：预测
上述数据框架包含了绘制地图所需的所有数据元素。
m.plot(forecast, plotting_backend="plotly-static"#plotting_backend = "matplotlib")
预测区间是由分位数值提供的！
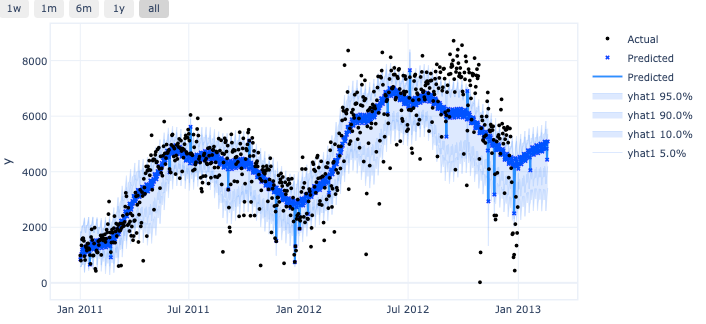图 (E)：分位数预测
预测区间和置信区间的区别
预测区间和置信区间在流行趋势中很有帮助，因为它们可以量化不确定性。它们的目标、计算方法和应用是不同的。下面我将用回归来解释两者的区别。在图(F)中，我在左边画出了线性回归，在右边画出了分位数回归。
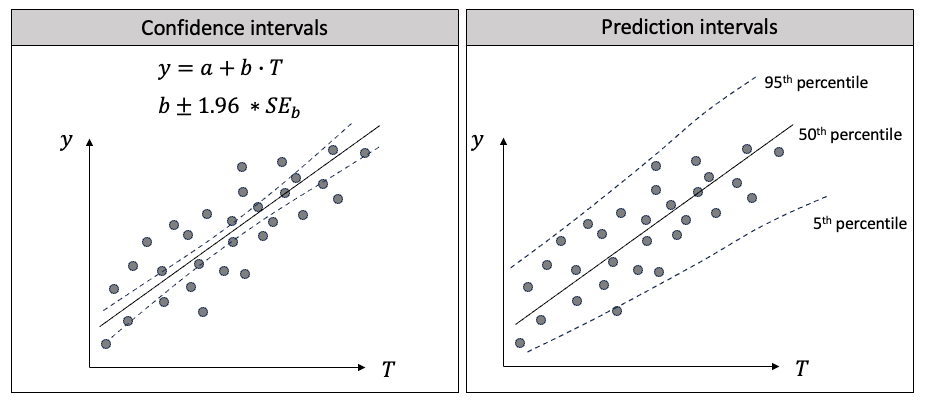图(F)：置信区间与预测区间的区别
首先，它们的目标不同：
- 线性回归的主要目标是找到一条线，使预测值尽可能接近给定自变量值时因变量的条件均值。
- 分位数回归旨在提供未来观测值的范围，在一定的置信度下。它估计自变量与因变量条件分布的不同量化值之间的关系。
其次，它们的计算方法不同：
- 在线性回归中，置信区间是对自变量系数的区间估计，通常使用普通最小二乘法 (OLS) 找出数据点到直线的最小总距离。系数的变化会影响预测的条件均值 Y。
- 在分位数回归中，你可以选择依赖变量的不同量级来估计回归系数，通常是最小化绝对偏差的加权和，而不是使用OLS方法。
第三，它们的应用不同：
- 在线性回归中，预测的条件均值有 95% 的置信区间。置信区间较窄，因为它是条件平均值，而不是整个范围。
- 在分位数回归中，预测值有 95% 的概率落在预测区间的范围内。
写在最后
本文介绍了分位数回归预测区间的概念，以及如何利用 NeuralProphet 生成预测区间。我们还强调了预测区间和置信区间之间的差异，这在商业应用中经常引起混淆。后面将继续探讨另一项重要的技术，即复合分位数回归（CQR），用于预测不确定性。
