导数和微分是微积分的基础内容,计算一元函数和多元函数的导数时,思想是一致的。无论是一元函数还是多元函数,导数和偏导数的计算都是将函数视为求导变量的一元函数进行求导。微分在描述形式上略有不同,但计算方法仍然相同,只是多元函数需要计算多个导数。
本文将通过具体实例,介绍如何利用线上工具计算具体和抽象函数的导数(包括偏导数)、微分以及多元函数的方向导数。
工具:Wolfram|Alpha 计算知识引擎,网址为:https://www.php.cn/link/f0e6d819eb9557e2fc97ac251d6bcd2a。

1、一元、多元函数一阶导数与导数值的计算

代码语言:javascript 代码运行次数:0
d/dx((x^3)cos(5x^2+e^(2x))-ln(3x^3-2x))
执行后的结果如下图所示。
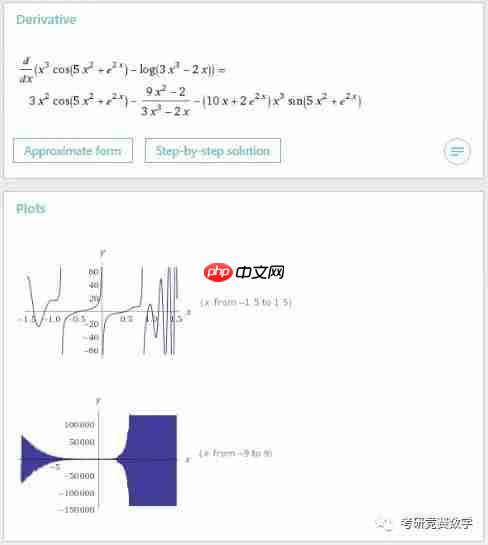
结果不仅显示导数结果,还给出了函数在不同范围内的图形。输入表达式也可以直接以更自然的语言描述形式输入,例如输入:
代码语言:javascript 代码运行次数:0
derivative of (x^3)cos(5x^2+e^(2x))-ln(3x^3-2x)
执行计算得到的结果一致。
在以上两种输入的表达式后面加上where x=1,例如输入:
代码语言:javascript 代码运行次数:0
derivative of (x^3)cos(5x^2+e^(2x))-ln(3x^3-2x) where x=1



2、一元、多元函数高阶导数的计算




3、抽象复合函数的一阶、高阶导数计算
将上面具体函数求导的函数表达式换成抽象函数即可。
例1 计算下列函数的一阶、二阶导数:
F(x) = x^2 f(3x + 4cos(x))
输入表达式为:
代码语言:javascript 代码运行次数:0
d/dx (x^2)f(3x+4cosx), d^2/dx^2 (x^2)f(3x+4cosx)
执行后的结果为:



4、全微分的计算


其中derivative可以替换为differential。也可以直接基于Wolfram语言,也即Mathematica中的命令来执行计算,例如输入表达式:
代码语言:javascript 代码运行次数:0
Dt(a sin(x^3+y^2)-(x+y^(1/2))^(1/2))
则将表达式中的符号都识别为变量符号,执行计算得到全微分表达式。如下图。


代码语言:javascript 代码运行次数:0
derivative x^3+y^3-3a x y=0 with respect to x
执行后的结果显示为:


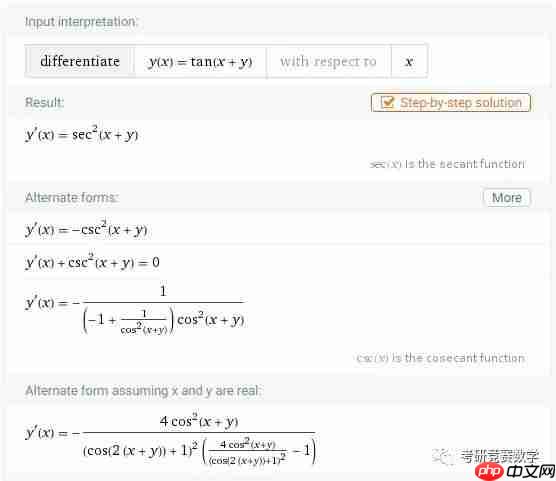

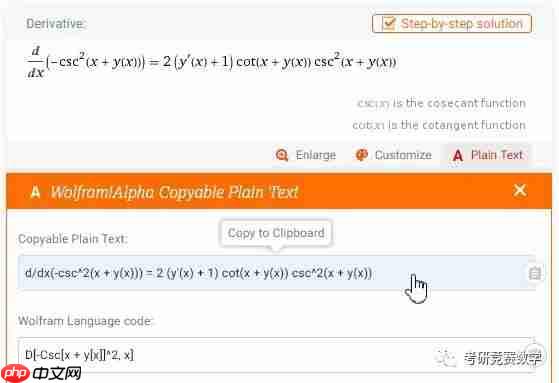


6、参数方程求一阶、二阶导数

代码语言:javascript 代码运行次数:0
(d/dt e^t sint)/(d/dt e^t cost)
执行后的结果显示为:

除了得到一阶导数结果外,当然还会显示一阶导函数很多各种相关的描述。
利用公式计算二阶导数,输入表达式为:
代码语言:javascript 代码运行次数:0
((d^2/dt^2 e^t sint)(d/dt e^t cost)-(d/dt e^t sint)(d^2/dt^2 e^t cost))/(d/dt e^t cost)^3
执行后的结果显示为:

7、方向导数的计算
例1 计算以下函数指定方向的方向导数:
f(x,y) = x e^(2y) + cos(xy), u = (3, -4)
输入表达式为:
代码语言:javascript 代码运行次数:0
derivative of x e^(2y)+cos(x y) in the direction (3,-4)
执行后的结果显示为:
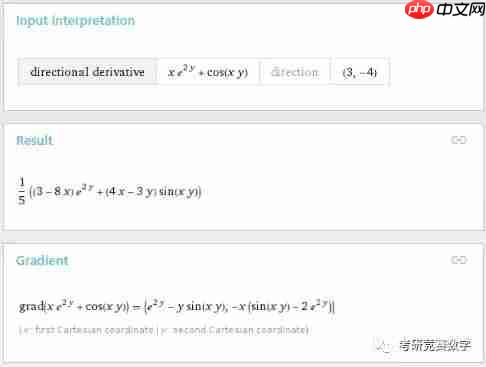
不仅给出了方向导数,也给出了函数的梯度向量。
例2 计算以下函数指定方向的方向导数:
z = f(x,y), u = (a,b)
输入表达式为:
代码语言:javascript 代码运行次数:0
derivative of f(x,y) in the direction (a,b)
执行后的结果显示为:

例3 计算以下函数指定方向和点处的方向导数:
f = 3x^2 + 2y^2 + z^2, u = (-2, -2, 1), P(1, 2, 3)
输入表达式为:
代码语言:javascript 代码运行次数:0
derivative 3x^2+2y^2+z^2 in direction (-2,-2,1) at point (1,2,3)
执行后的结果显示为:

当然,以上计算也可以直接依据求偏导数与方向导数计算公式,逐步计算代入得到结果。






























