本文为深度学习训练篇，先以Paddle2.0框架实现手写数字识别训练，再从理论讲解前向传播、损失函数等，接着解析训练过程代码，包括模式切换、优化器定义等，还介绍模型推理及用VisualDL进行可视化，助新手理解训练。
☞☞☞AI 智能聊天, 问答助手, AI 智能搜索, 免费无限量使用 DeepSeek R1 模型☜☜☜
深度学习三步走（三）训练篇
很多新手小白对于训练这一阶段总是没有理清楚，本篇文章就来讲讲训练是怎么完成的以及代码实战。
In [2]
from paddle.vision.transforms import Compose, Normalizeimport paddleimport paddle.nn.functional as F
transform = Compose([Normalize(mean=[127.5],
std=[127.5],
data_format='CHW')])# 使用transform对数据集做归一化print('download training data and load training data')
train_dataset = paddle.vision.datasets.MNIST(mode='train', transform=transform)
test_dataset = paddle.vision.datasets.MNIST(mode='test', transform=transform)print('load finished')class LeNet(paddle.nn.Layer):
def __init__(self):
super(LeNet, self).__init__()
self.conv1 = paddle.nn.Conv2D(in_channels=1, out_channels=6, kernel_size=5, stride=1, padding=2)
self.max_pool1 = paddle.nn.MaxPool2D(kernel_size=2, stride=2)
self.conv2 = paddle.nn.Conv2D(in_channels=6, out_channels=16, kernel_size=5, stride=1)
self.max_pool2 = paddle.nn.MaxPool2D(kernel_size=2, stride=2)
self.linear1 = paddle.nn.Linear(in_features=16*5*5, out_features=120)
self.linear2 = paddle.nn.Linear(in_features=120, out_features=84)
self.linear3 = paddle.nn.Linear(in_features=84, out_features=10) def forward(self, x):
x = self.conv1(x)
x = F.relu(x)
x = self.max_pool1(x)
x = self.conv2(x)
x = F.relu(x)
x = self.max_pool2(x)
x = paddle.flatten(x, start_axis=1,stop_axis=-1)
x = self.linear1(x)
x = F.relu(x)
x = self.linear2(x)
x = F.relu(x)
x = self.linear3(x) return x
train_loader = paddle.io.DataLoader(train_dataset, batch_size=64, shuffle=True)# 加载训练集 batch_size 设为 64def train(model):
model.train()
epochs = 2
optim = paddle.optimizer.Adam(learning_rate=0.001, parameters=model.parameters()) # 用Adam作为优化函数
for epoch in range(epochs): for batch_id, data in enumerate(train_loader()):
x_data = data[0]
y_data = data[1]
predicts = model(x_data)
loss = F.cross_entropy(predicts, y_data) # 计算损失
acc = paddle.metric.accuracy(predicts, y_data)
loss.backward() if batch_id % 300 == 0: print("epoch: {}, batch_id: {}, loss is: {}, acc is: {}".format(epoch, batch_id, loss.numpy(), acc.numpy()))
optim.step()
optim.clear_grad()
model = LeNet()
train(model)
download training data and load training data load finished epoch: 0, batch_id: 0, loss is: [2.8969913], acc is: [0.140625] epoch: 0, batch_id: 300, loss is: [0.2108319], acc is: [0.9375] epoch: 0, batch_id: 600, loss is: [0.08061229], acc is: [0.953125] epoch: 0, batch_id: 900, loss is: [0.1136723], acc is: [0.9375] epoch: 1, batch_id: 0, loss is: [0.13105258], acc is: [0.953125] epoch: 1, batch_id: 300, loss is: [0.02431063], acc is: [1.] epoch: 1, batch_id: 600, loss is: [0.04277265], acc is: [0.984375] epoch: 1, batch_id: 900, loss is: [0.05149914], acc is: [0.96875]
一、理论篇
1.1 前向传播
我们把神经网络每一层分为三类 输入层、隐含层、输出层
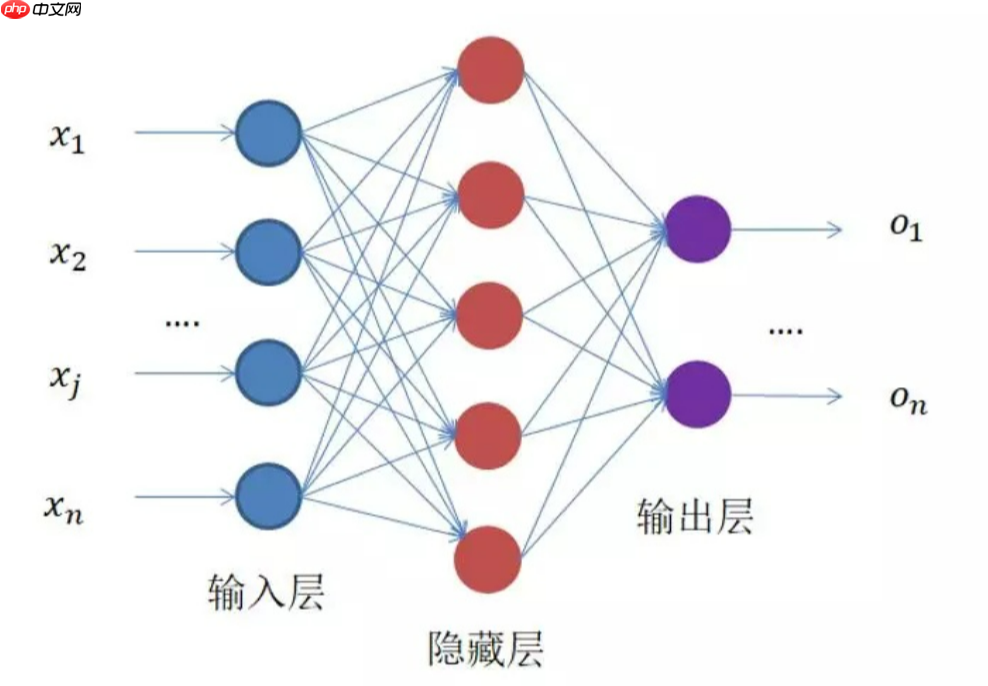
数据作为输入送到输入层，输入层的输出作为隐含层的输入，然后隐含层的输出作为输出层的输入，然后得到最终输出结果。
1.2损失函数
1、均方差损失--MSE
均方差损失一般是用于回归问题，均方差损失的定义如下：
$L(s,y) = \frac{1}{n}\sum_{t=1}^{n}(s_{t}- y_{t})^{2} $
其中y为标签值，s为网络前向传播的预测值
2、交叉熵损失--CrossEntropyloss
交叉熵损失一般用于分类问题，在分类问题中，一般使用softmax函数作为输出层的激活函数，首先介绍一下softmax函数。
多分类问题（分类种类为t个）在经过输出层的计算后，会产生t个输出，softmax的作用就是将输出x转化为和为1的概率问题。其定义如下：
$s_{i}=\frac{e^{x_{i} } }{ {\textstyle \sum_{i=1}^{t}}e^{x_{i} } } $
交叉熵损失的定义如下：
$C(y,s)=-\sum_{i=1}^{t}y_{i}ln(s_{i} ) $
此处的si即为softmax处理后的si。
其反向传播过程也比较好算，在这用一个例子来具体解释一下交叉熵在多分类问题的应用。
给定一个猫的图片，我们想要制作一个三分类的分类器，分别有猫、狗、鼠三个类别，在训练过程中，当我们输入一个猫的图片后，经过网络的前向传播（输出层的激活函数为softmax），我们可以得到这样一个输出[0.6,0.1,0.3]，我们的标签数据为[1，0，0]。此时可以计算得到交叉熵损失为：
带入公式
C=−(1∗ln(0.426))=0.85
这里0.426是经过了softmax函数换算过来的
可以看到，当准确率越大时，对应的交叉熵损失就会越小。
1.3 优化器
在深度学习中，不同的优化器只是定义了不同的一阶动量和二阶动量，一阶动量是与梯度相关的函数，二阶动量是与梯度平方相关的函数。常用的优化器主要有随机梯度下降法、Momentum、AdaGrad、RMSProp和Adam优化器。
随机梯度下降
目前，神经网络最常用的为随机梯度下降（Stochastic Gradient Descent，SGD），其基本思想是将数据分成n个样本，通过计算各自梯度的平均值来更新梯度，即对网络参数w更新过程中不需要全部遍历整个样本，而是只看一个训练样本（batch size）使用梯度下降进行更新，然后利用下一个样本进行下一次更新。 SGD简单且容易实现，解决了随机小批量样本的问题，由于只对一个训练样本进行梯度下降，可以提高网络参数的更新速度；但其训练时下降速度慢、准确率下降、容易陷入局部最优以及不容易实现并行处理等问题。
Adam 优化器
Adam是将Momentum与RMSProp结合起来的一种算法，引入了Momentum的一阶动量来累计梯度与RMSProp的二阶动量可以使得收敛速度快的同时使得波动幅度小，然后在此基础上增加了两个修正项，能够实现参数自新。 Adam优化器具有以下优点：
1、实现简单，计算高效，对内存需求少
2、参数的更新不受梯度的伸缩变换影响
3、超参数具有很好的解释性，且通常无需调整或仅需很少的微调
4、更新的步长能够被限制在大致的范围内（初始学习率）
5、能自然地实现步长退火过程（自动调整学习率）
6、很适合应用于大规模的数据及参数的场景
7、适用于不稳定目标函数
8、适用于梯度稀疏或梯度存在很大噪声的问题
1.4 反向传播
经过了前向传播，得到了一个输出结果r1，但是我们希望神经网络得到的是r2，所以这里应用损失函数
loss=f(r1,r2)
神经网络利用优化器来更新网络参数步骤如下：
（一）计算当前时刻t损失函数关于网络参数w的梯度
$g_t= \bigtriangledown loss=\frac{\partial loss}{\partial (w_{t} )} $
（二）计算当前时刻t一阶动量mt和二阶动量Vt
（三）计算当前时刻t下降梯度
$ n_t=lr.m_t/\sqrt{v_t}$
（四）计算下一时刻t+1参数
$ w_{t+1}=w_t-n_t=w_t-lr.m_t/\sqrt{v_t} $
二、实战篇
快速实现
运行下方代码，快速实现模型组网，本次网络采用经典Lenet网络,首先定义网络结构
In [3]
import paddleimport paddle.nn.functional as Fclass LeNet(paddle.nn.Layer):
def __init__(self):
super(LeNet, self).__init__()
self.conv1 = paddle.nn.Conv2D(in_channels=1, out_channels=6, kernel_size=5, stride=1, padding=2)
self.max_pool1 = paddle.nn.MaxPool2D(kernel_size=2, stride=2)
self.conv2 = paddle.nn.Conv2D(in_channels=6, out_channels=16, kernel_size=5, stride=1)
self.max_pool2 = paddle.nn.MaxPool2D(kernel_size=2, stride=2)
self.linear1 = paddle.nn.Linear(in_features=16*5*5, out_features=120)
self.linear2 = paddle.nn.Linear(in_features=120, out_features=84)
self.linear3 = paddle.nn.Linear(in_features=84, out_features=10) def forward(self, x):
x = self.conv1(x)
x = F.relu(x)
x = self.max_pool1(x)
x = self.conv2(x)
x = F.relu(x)
x = self.max_pool2(x)
x = paddle.flatten(x, start_axis=1,stop_axis=-1)
x = self.linear1(x)
x = F.relu(x)
x = self.linear2(x)
x = F.relu(x)
x = self.linear3(x) return x
In [4]
model = LeNet() data = paddle.randn(shape=(32, 1, 28, 28), ) result = model(data)print(result.reshape)
开始训练
定义网络并确定输入输出，运行下方代码，搭配注释对训练过程进行一个初步的了解,这里数据采用的是随机数，具体数据可由实际生成而定
In [5]
import paddle.nn.functional as Fimport numpy as np
train_data = 500model = LeNet()# 加载训练集 batch_size 设为 64model.train() # 切换到训练模式epochs = 5 # 设置迭代次数optim = paddle.optimizer.Adam(learning_rate=0.001, parameters=model.conv1.parameters()) # 定义优化器
# 用Adam作为优化函数for epoch in range(epochs): # 开始进入迭代循环
for batch_id in range(train_data): # 开始提取数据，这里数据采取随机数据
paddle.seed(batch_id) # 设置随机数种子
x_data = paddle.randn(shape=(1,1,28,28)) # 神经网络输入数据
y_data = paddle.randint(0, 10, shape=[1,1], dtype="int64") # 预期得到的数据
# print(x_data.shape,y_data.shape)
predicts = model(x_data) # 经过前向传播得到的数据
# print(predicts.shape)
# print(predicts,y_data)
loss = F.cross_entropy(predicts, y_data) # 将前向传播得到的数据和预期得到的数据通过损失函数计算得到误差loss
# 计算损失
acc = paddle.metric.accuracy(predicts, y_data) # 调用paddle中函数直接求准确率得到acc
loss.backward() # 进行误差反向传播
if batch_id % 300 == 0: print("epoch: {}, batch_id: {}, loss is: {}, acc is: {}".format(epoch, batch_id, loss.numpy(), acc.numpy()))
optim.step() # 开始更新参数
optim.clear_grad() # 梯度清0，开始下一批次
epoch: 0, batch_id: 0, loss is: [10.199537], acc is: [0.] epoch: 0, batch_id: 300, loss is: [1.947201], acc is: [0.] epoch: 1, batch_id: 0, loss is: [6.0519843], acc is: [0.] epoch: 1, batch_id: 300, loss is: [2.0437965], acc is: [0.] epoch: 2, batch_id: 0, loss is: [4.007648], acc is: [0.] epoch: 2, batch_id: 300, loss is: [2.1998882], acc is: [0.] epoch: 3, batch_id: 0, loss is: [3.1512375], acc is: [0.] epoch: 3, batch_id: 300, loss is: [2.2498567], acc is: [0.] epoch: 4, batch_id: 0, loss is: [2.7662919], acc is: [0.] epoch: 4, batch_id: 300, loss is: [2.3091187], acc is: [0.]
2.1 训练模式和评估模式
接下来从代码层面解析一下神经网络训练的过程 首先切换到训练模式
model.train()
在深度学习训练中，有两种训练模式model.train()和model.eval() 当处于训练模式的时候，参数会随着训练进行一个更新，其中 Batch Normalization 和 Dropout等防止过拟合等手段都发挥作用
当处于评估模式时，参数就属于固定状态，BN层采用的均值和方差都是固定的，不要变化了，同时Dropout 层不起作用。
2.2 定义优化器
优化器是引导神经网络更新参数的工具，深度学习在计算出损失函数之后，需要利用优化器来进行反向传播，完成网络参数的更新。在这个过程中，便会使用到优化器，优化器可以利用计算机数值计算的方法来获取损失函数最小的网络参数。在深度学习中，不同的优化器只是定义了不同的一阶动量和二阶动量，一阶动量是与梯度相关的函数，二阶动量是与梯度平方相关的函数。常用的优化器主要有随机梯度下降法、Momentum、AdaGrad、RMSProp和Adam优化器。
optim = paddle.optimizer.Adam(learning_rate=0.001, parameters=model.parameters()) # 定义优化器
这里定义了Adam优化器，需要的参数
learing_rate: 学习率
parameters: 指定优化器需要优化的参数。在动态图模式下必须提供该参数；在静态图模式下默认值为None，这时所有的参数都将被优化。 这里可以指定更新某个网络层的参数，比如，
optim = paddle.optimizer.Adam(learning_rate=0.001, parameters=model.conv1.parameters()) # 定义优化器
这一段指定更新第一个卷积的参数 对于图像分类网络，我们可以固定卷积层只训练全连接层，可以大大提升训练的速度
2.3 导入数据
首先确定模型输入和输出，从对模型Lenet网络测试可以得到输入
输入张量形状：（1，1，28，28）
输出张量形状：（1，10）
这里暂时伪造数据
x_data = paddle.randn(shape=(1,1,28,28)) # 神经网络输入数据y_data = paddle.randint(0, 10, shape=[1,1], dtype="int64")# 预期得到的数据
size>
2.4 计算损失
将数据导入模型中得到预测值
predicts = model(x_data) # 经过前向传播得到的数据
将预测值和实际值作为输入计算得到的损失 这里采用的交叉熵损失函数
loss = F.cross_entropy(predicts, y_data)
在paddle.nn.functional库中用很多损失函数
2.5 反向传播更新参数
我们得到损失值loss，调用backward方法，实现反向传播
loss.backward()
接下来开始通过优化器更新参数
optim.step()
然后进行梯度清0
optim.clear_grad() # 梯度清0，开始下一批次
这里问题来了,为什么要梯度清0，在训练的时候，如果不清0，梯度就会在下一个批次进行累加，在网络进行反馈的时，梯度不是替换而是累加，所以在每一个梯度更新后，就要进行一个梯度清0。
到这里，一批次的训练和参数的更新就完成了
三、模型推理
上面完成了一个基础训练，问题来了，该如何去保存训练更新的参数和模型文件，paddle提供了保存模型参数文件的函数，接下来细细道来
paddle.save(layer.state_dict(), "linear_net.pdparams") paddle.save(adam.state_dict(), "adam.pdopt")
运行就可以得到模型文件和参数文件了
In [6]
paddle.save(model.state_dict(), "Lenet.pdparams") paddle.save(optim.state_dict(), "optim.pdopt")
保存完文件，我们需要加载文件，加载参数和模型可以调用load函数
layer_state_dict = paddle.load("Lenet.pdparams")
opt_state_dict = paddle.load("optim.pdopt")
model.set_state_dict(layer_state_dict)optim.set_state_dict(opt_state_dict)
In [7]
layer_state_dict = paddle.load("Lenet.pdparams")
opt_state_dict = paddle.load("optim.pdopt")
model.set_state_dict(layer_state_dict)
optim.set_state_dict(opt_state_dict)# 参数加载完成
In [8]
model.eval() # 切换到评估模式x_data_start = paddle.randn(shape=(1,1,28,28)) predicts = model(x_data_start) # 经过前向传播得到的数据print(predicts)# 得到预测结果
Tensor(shape=[1, 10], dtype=float32, place=Place(gpu:0), stop_gradient=False,
[[ 0.14132717, 1.10214913, -0.08096960, -0.23006104, 0.12370837,
0.04107335, 0.13364884, 0.08352894, 0.04745370, -0.31018108]])
四、可视化
VisualDL是PaddlePaddle的可视化分析工具，提供多种图表来展示参数趋势，将模型结构、数据样本、张量直方图、PR曲线、ROC曲线和高维数据分布可视化。让用户更清晰直观地了解训练过程和模型结构，从而高效优化模型。
VisualDL提供多种可视化功能，包括实时跟踪metrics、可视化模型结构、展示数据样本、可视化超参数与模型metrics之间的关系、呈现张量分布的变化、展示pr曲线、投影高维数据到低维空间等等。此外，VisualDL 提供 VDL.service，使开发人员能够轻松地保存、跟踪和共享实验的可视化结果。每个功能的具体指导，请参考 VisualDL 用户指南。如需最新体验，请随时尝试我们的在线演示。目前，VisualDL 迭代速度很快，新功能会不断增加。
VisualDL使用指南：https://github.com/PaddlePaddle/VisualDL/blob/develop/README.md
修改使用指南中的示例 ：
from visualdl import LogWriter # 引入头文件 writer = LogWriter(logdir="./log/scalar_test/train") # 建立日志文件夹# use `add_scalar` to record scalar valueswriter.add_scalar(tag="acc", step=1, value=0.5678) # 往日志里写入数据 writer.add_scalar(tag="acc", step=2, value=0.6878) writer.add_scalar(tag="acc", step=3, value=0.9878)
实战操作： 在训练时有两个循环，第一个循环
for epoch in range(epochs):
在训练之前添加日志文件夹,当Loss得到时，可以
writer = LogWriter(logdir="./log") # 建立日志文件夹 for epoch in range(epochs): ...
writer.add_scalar(tag="loss", step=1, value=0.5678) # 往日志里写入数据
接下来结合代码进行操作一下
In [5]
import numpy as npimport paddleimport paddle.nn as nnimport paddle.nn.functional as Ffrom paddle.vision.transforms import Compose, Normalizefrom paddle.metric import Accuracyfrom visualdl import LogWriter # 引入头文件class Lenet(nn.Layer):
# 卷积计算公式
# (x+2*p-k)/stride + 1
# 池化计算公式
def __init__(self, in_dim=3, out_dim=3,num_class=10):
super(Lenet, self).__init__() # 第一层卷积
self.conv1 = nn.Conv2D(in_channels=in_dim, out_channels=out_dim, kernel_size=3, stride=1, padding=1)
self.maxpool1 = nn.MaxPool2D(2)
self.conv2 = nn.Conv2D(in_channels=out_dim, out_channels=out_dim, kernel_size=3, stride=1, padding=1)
self.maxpool2 = nn.MaxPool2D(2)
self.Relu = nn.ReLU()
self.Flatten = nn.Flatten()
self.linear1 = nn.Linear(out_dim * 8 * 8, 1024)
self.linear2 = nn.Linear(1024, 10)
self.last_conv = nn.Conv2D(in_channels=out_dim,out_channels=num_class,kernel_size=1,stride=1)
self.GAP = nn.AdaptiveMaxPool2D(output_size=1, return_mask=False) def forward(self, x):
x = self.conv1(x)
x = self.maxpool1(x)
x = self.conv2(x)
x = self.maxpool2(x) # x = self.last_conv(x)
# x = self.GAP(x)
x = self.Flatten(x)
x = self.linear1(x)
x = self.linear2(x) return x# 参数配置lr = 0.001batch_size = 64# 定义数据增强transform = Compose([Normalize(mean=[127.5],
std=[127.5],
data_format='CHW')])# 数据加载train_dataset = paddle.vision.datasets.Cifar10(mode="train", transform=transform)
test_loader = paddle.vision.datasets.Cifar10(mode="test", transform=transform)print("data load finished")
model = Lenet()
epochs = 20optim = paddle.optimizer.Adam(learning_rate=0.001, parameters=model.parameters())
train_loader = paddle.io.DataLoader(train_dataset, batch_size=32, shuffle=True)
writer = LogWriter(logdir="./log") # 建立日志文件夹 *********************改动地方*******************************for epoch in range(epochs): for batch_id, data in enumerate(train_loader()):
x_data = data[0]
x_data = paddle.transpose(x_data, perm=[0, 3, 1, 2])
y_data = data[1]
y_data = y_data[:,np.newaxis] # print(x_data.shape, y_data.shape)
# print(type(x_data))
predicts = model(x_data) # print(predicts.shape)
# predicts = predicts[:,:,0,0]
# print(predicts.shape)
loss = F.cross_entropy(predicts, y_data) # 计算损失
acc = paddle.metric.accuracy(predicts, y_data)
loss.backward() if batch_id % 300 == 0: print("epoch: {}, batch_id: {}, loss is: {}, acc is: {}".format(epoch, batch_id, loss.numpy(), acc.numpy()))
optim.step()
optim.clear_grad()
writer.add_scalar(tag="loss", step=epoch, value=loss.numpy()) # 往日志里写入数据
writer.add_scalar(tag="acc", step=epoch, value=acc.numpy()) # 往日志里写入数据
data load finished epoch: 0, batch_id: 0, loss is: [2.7075284], acc is: [0.09375] epoch: 0, batch_id: 300, loss is: [1.7044138], acc is: [0.34375] epoch: 0, batch_id: 600, loss is: [1.3984089], acc is: [0.4375] epoch: 0, batch_id: 900, loss is: [1.5114894], acc is: [0.40625] epoch: 0, batch_id: 1200, loss is: [1.8019118], acc is: [0.34375] epoch: 0, batch_id: 1500, loss is: [2.1451519], acc is: [0.25] epoch: 1, batch_id: 0, loss is: [1.5192074], acc is: [0.53125] epoch: 1, batch_id: 300, loss is: [1.8006582], acc is: [0.34375] epoch: 1, batch_id: 600, loss is: [1.2446223], acc is: [0.5] epoch: 1, batch_id: 900, loss is: [1.7084994], acc is: [0.375] epoch: 1, batch_id: 1200, loss is: [2.0738], acc is: [0.34375] epoch: 1, batch_id: 1500, loss is: [1.7818656], acc is: [0.3125] epoch: 2, batch_id: 0, loss is: [1.5525913], acc is: [0.4375] epoch: 2, batch_id: 300, loss is: [1.4675462], acc is: [0.46875] epoch: 2, batch_id: 600, loss is: [1.5895747], acc is: [0.4375] epoch: 2, batch_id: 900, loss is: [1.6101584], acc is: [0.46875] epoch: 2, batch_id: 1200, loss is: [1.3697554], acc is: [0.59375] epoch: 2, batch_id: 1500, loss is: [1.4336786], acc is: [0.46875] epoch: 3, batch_id: 0, loss is: [0.9415606], acc is: [0.65625] epoch: 3, batch_id: 300, loss is: [1.5181022], acc is: [0.53125] epoch: 3, batch_id: 600, loss is: [1.4998069], acc is: [0.5] epoch: 3, batch_id: 900, loss is: [1.5309279], acc is: [0.5] epoch: 3, batch_id: 1200, loss is: [1.3324285], acc is: [0.46875] epoch: 3, batch_id: 1500, loss is: [1.2474538], acc is: [0.5] epoch: 4, batch_id: 0, loss is: [1.4426242], acc is: [0.53125] epoch: 4, batch_id: 300, loss is: [1.3277245], acc is: [0.5625] epoch: 4, batch_id: 600, loss is: [1.4224291], acc is: [0.53125] epoch: 4, batch_id: 900, loss is: [1.7937247], acc is: [0.5] epoch: 4, batch_id: 1200, loss is: [1.5001082], acc is: [0.4375] epoch: 4, batch_id: 1500, loss is: [1.8181291], acc is: [0.3125] epoch: 5, batch_id: 0, loss is: [2.3011112], acc is: [0.28125] epoch: 5, batch_id: 300, loss is: [1.429127], acc is: [0.4375] epoch: 5, batch_id: 600, loss is: [1.4246702], acc is: [0.46875] epoch: 5, batch_id: 900, loss is: [1.2299116], acc is: [0.5625] epoch: 5, batch_id: 1200, loss is: [1.7141062], acc is: [0.375] epoch: 5, batch_id: 1500, loss is: [1.3357327], acc is: [0.46875] epoch: 6, batch_id: 0, loss is: [1.2410089], acc is: [0.53125] epoch: 6, batch_id: 300, loss is: [1.2839394], acc is: [0.65625] epoch: 6, batch_id: 600, loss is: [1.3473102], acc is: [0.5625] epoch: 6, batch_id: 900, loss is: [1.0759284], acc is: [0.625] epoch: 6, batch_id: 1200, loss is: [1.1812735], acc is: [0.5625] epoch: 6, batch_id: 1500, loss is: [1.4892402], acc is: [0.40625] epoch: 7, batch_id: 0, loss is: [1.0520734], acc is: [0.65625] epoch: 7, batch_id: 300, loss is: [1.3992872], acc is: [0.4375] epoch: 7, batch_id: 600, loss is: [1.5899432], acc is: [0.4375] epoch: 7, batch_id: 900, loss is: [1.2754831], acc is: [0.53125] epoch: 7, batch_id: 1200, loss is: [1.2994168], acc is: [0.59375] epoch: 7, batch_id: 1500, loss is: [1.2096431], acc is: [0.65625] epoch: 8, batch_id: 0, loss is: [1.5027049], acc is: [0.53125] epoch: 8, batch_id: 300, loss is: [1.4931258], acc is: [0.46875] epoch: 8, batch_id: 600, loss is: [1.95404], acc is: [0.4375] epoch: 8, batch_id: 900, loss is: [1.4669464], acc is: [0.59375] epoch: 8, batch_id: 1200, loss is: [1.3580099], acc is: [0.5] epoch: 8, batch_id: 1500, loss is: [1.4240929], acc is: [0.5] epoch: 9, batch_id: 0, loss is: [1.5138721], acc is: [0.5] epoch: 9, batch_id: 300, loss is: [1.4442466], acc is: [0.625] epoch: 9, batch_id: 600, loss is: [1.5553632], acc is: [0.4375] epoch: 9, batch_id: 900, loss is: [1.2714009], acc is: [0.5625] epoch: 9, batch_id: 1200, loss is: [1.5337567], acc is: [0.5] epoch: 9, batch_id: 1500, loss is: [1.1937754], acc is: [0.59375] epoch: 10, batch_id: 0, loss is: [1.1503779], acc is: [0.59375] epoch: 10, batch_id: 300, loss is: [1.2517458], acc is: [0.5] epoch: 10, batch_id: 600, loss is: [1.0282918], acc is: [0.6875] epoch: 10, batch_id: 900, loss is: [1.344882], acc is: [0.4375] epoch: 10, batch_id: 1200, loss is: [1.70032], acc is: [0.34375] epoch: 10, batch_id: 1500, loss is: [1.38028], acc is: [0.53125] epoch: 11, batch_id: 0, loss is: [1.5775305], acc is: [0.5] epoch: 11, batch_id: 300, loss is: [1.433978], acc is: [0.59375] epoch: 11, batch_id: 600, loss is: [1.4946765], acc is: [0.4375] epoch: 11, batch_id: 900, loss is: [1.6713679], acc is: [0.4375] epoch: 11, batch_id: 1200, loss is: [1.4650068], acc is: [0.5625] epoch: 11, batch_id: 1500, loss is: [1.2745992], acc is: [0.46875] epoch: 12, batch_id: 0, loss is: [1.1843674], acc is: [0.5] epoch: 12, batch_id: 300, loss is: [1.5598009], acc is: [0.46875] epoch: 12, batch_id: 600, loss is: [1.5697795], acc is: [0.375] epoch: 12, batch_id: 900, loss is: [1.5500634], acc is: [0.53125] epoch: 12, batch_id: 1200, loss is: [0.9000268], acc is: [0.6875] epoch: 12, batch_id: 1500, loss is: [1.2567226], acc is: [0.5625] epoch: 13, batch_id: 0, loss is: [1.484086], acc is: [0.40625] epoch: 13, batch_id: 300, loss is: [1.2141889], acc is: [0.5625] epoch: 13, batch_id: 600, loss is: [1.6185546], acc is: [0.5] epoch: 13, batch_id: 900, loss is: [1.6308584], acc is: [0.34375] epoch: 13, batch_id: 1200, loss is: [1.493471], acc is: [0.53125] epoch: 13, batch_id: 1500, loss is: [1.3990285], acc is: [0.5625] epoch: 14, batch_id: 0, loss is: [1.174399], acc is: [0.65625] epoch: 14, batch_id: 300, loss is: [1.396074], acc is: [0.5] epoch: 14, batch_id: 600, loss is: [1.3281026], acc is: [0.625] epoch: 14, batch_id: 900, loss is: [1.7970767], acc is: [0.46875] epoch: 14, batch_id: 1200, loss is: [1.041579], acc is: [0.625] epoch: 14, batch_id: 1500, loss is: [1.2198353], acc is: [0.59375] epoch: 15, batch_id: 0, loss is: [1.5300723], acc is: [0.625] epoch: 15, batch_id: 300, loss is: [1.4993348], acc is: [0.65625] epoch: 15, batch_id: 600, loss is: [1.1719993], acc is: [0.5] epoch: 15, batch_id: 900, loss is: [1.3079828], acc is: [0.5625] epoch: 15, batch_id: 1200, loss is: [1.3641269], acc is: [0.53125] epoch: 15, batch_id: 1500, loss is: [1.3562933], acc is: [0.5625] epoch: 16, batch_id: 0, loss is: [1.4652226], acc is: [0.5625] epoch: 16, batch_id: 300, loss is: [1.6116624], acc is: [0.46875] epoch: 16, batch_id: 600, loss is: [1.4096103], acc is: [0.5] epoch: 16, batch_id: 900, loss is: [1.6114434], acc is: [0.40625] epoch: 16, batch_id: 1200, loss is: [1.8129449], acc is: [0.34375] epoch: 16, batch_id: 1500, loss is: [1.2892506], acc is: [0.53125] epoch: 17, batch_id: 0, loss is: [1.6298327], acc is: [0.46875] epoch: 17, batch_id: 300, loss is: [1.4053156], acc is: [0.40625] epoch: 17, batch_id: 600, loss is: [1.5590739], acc is: [0.5] epoch: 17, batch_id: 900, loss is: [1.3113258], acc is: [0.40625] epoch: 17, batch_id: 1200, loss is: [1.6673313], acc is: [0.375] epoch: 17, batch_id: 1500, loss is: [1.4234462], acc is: [0.5] epoch: 18, batch_id: 0, loss is: [1.4010768], acc is: [0.40625] epoch: 18, batch_id: 300, loss is: [1.4580048], acc is: [0.4375] epoch: 18, batch_id: 600, loss is: [1.3012905], acc is: [0.53125] epoch: 18, batch_id: 900, loss is: [1.6653962], acc is: [0.5] epoch: 18, batch_id: 1200, loss is: [1.421701], acc is: [0.46875] epoch: 18, batch_id: 1500, loss is: [1.3961929], acc is: [0.53125] epoch: 19, batch_id: 0, loss is: [0.96382546], acc is: [0.6875] epoch: 19, batch_id: 300, loss is: [1.633214], acc is: [0.5] epoch: 19, batch_id: 600, loss is: [1.5573952], acc is: [0.40625] epoch: 19, batch_id: 900, loss is: [1.350167], acc is: [0.625] epoch: 19, batch_id: 1200, loss is: [1.2849283], acc is: [0.53125] epoch: 19, batch_id: 1500, loss is: [1.4163616], acc is: [0.65625]
4.2 运行VDL工具
首先运行完成后，参数信息保存在log文件夹中，如图，在文件夹中生成了日志信息，接下来我们利用BML中的VDL工具来解析一下这个.log文件
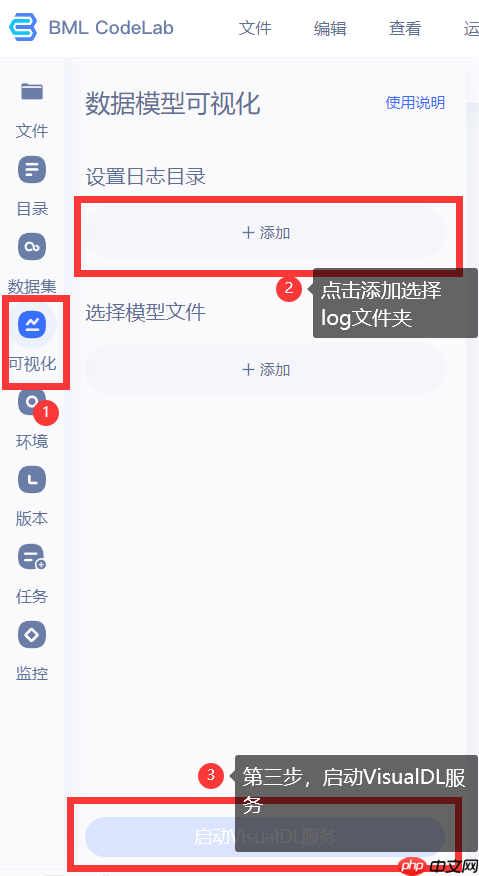
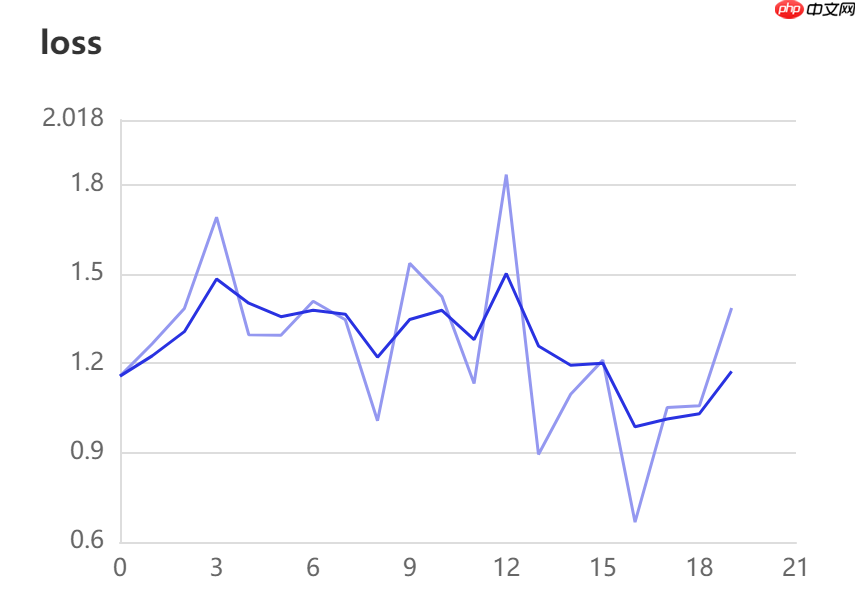
接下来点击进入VisualDL，会新开一个界面，进入到可视化界面，如下图
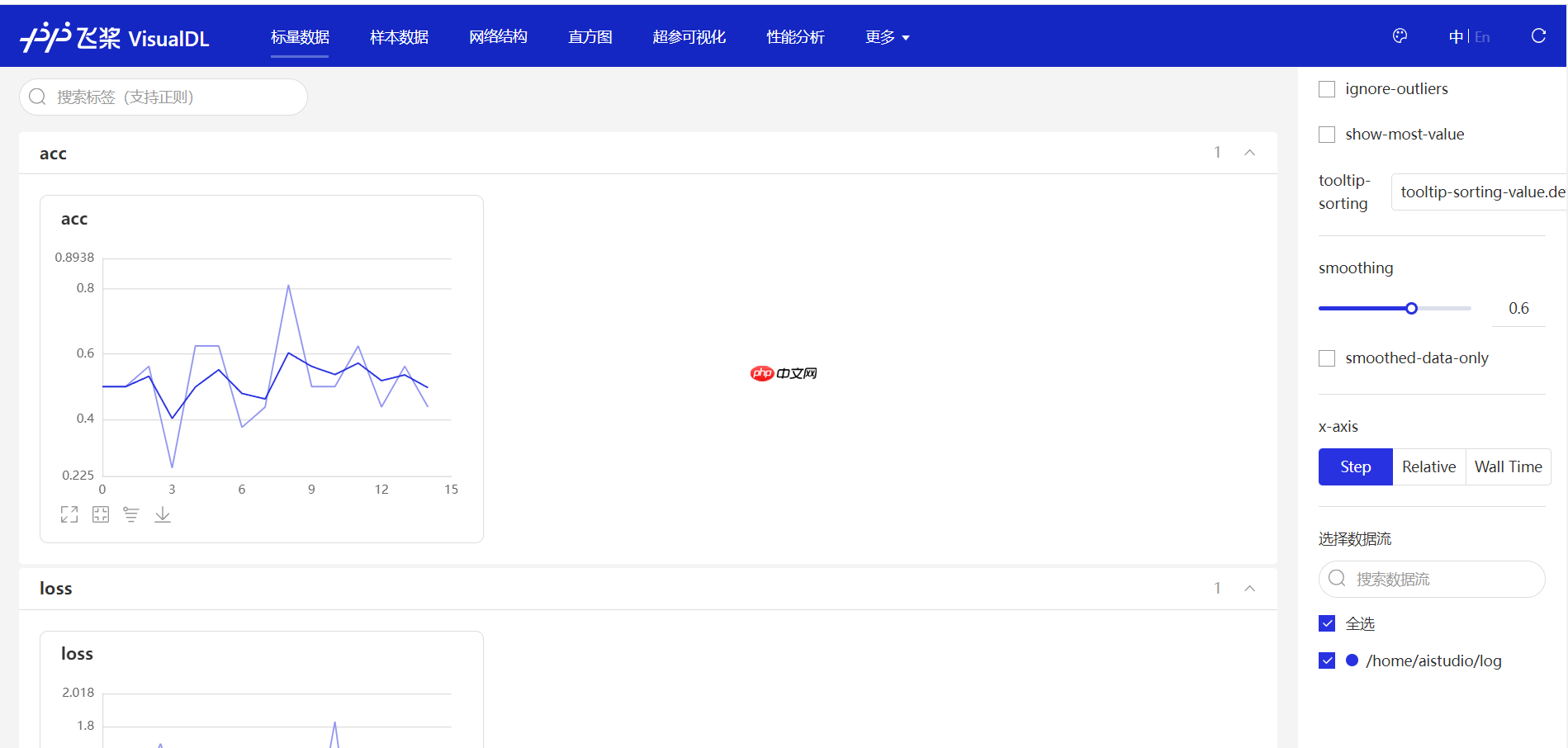
在图上有两个指标，正好和我们在代码中写的一样，acc和loss指标。合理设计，即可对参数进行一个可视化
**
In [ ]
