前面所讨论的线性表元素之间都是一对一的关系,今天我们所看到的结构各元素之间却是一对多的关系。树在计算机中有着广泛的应用,甚至在计算机的日常使用中,也可以看到树形结构的身影,如下图所示的windows资源管理器和应用程序的菜单都属于树形结构。树形结构是一种典型的非线性结构,除了用于表示相邻关系外,还可以表示层次关系。本文重点讨论树与二叉树的基本结构和遍历算法等内容。
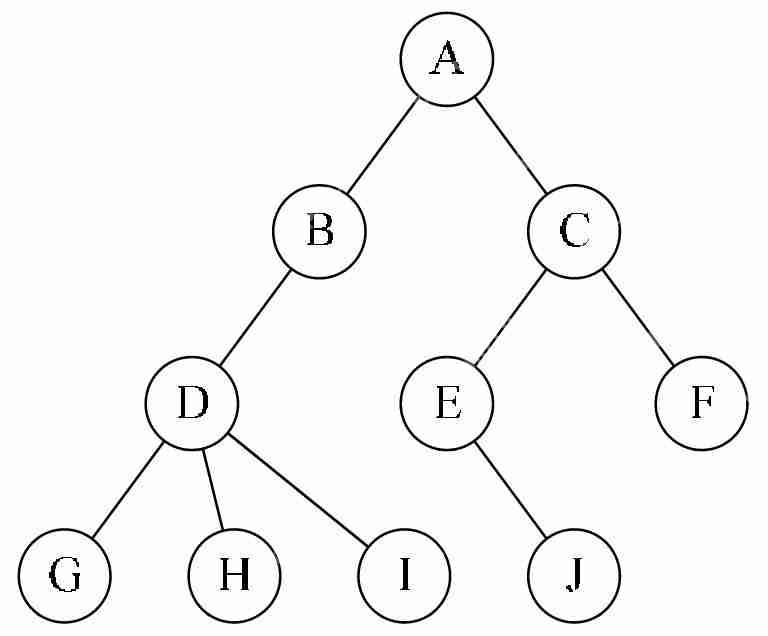
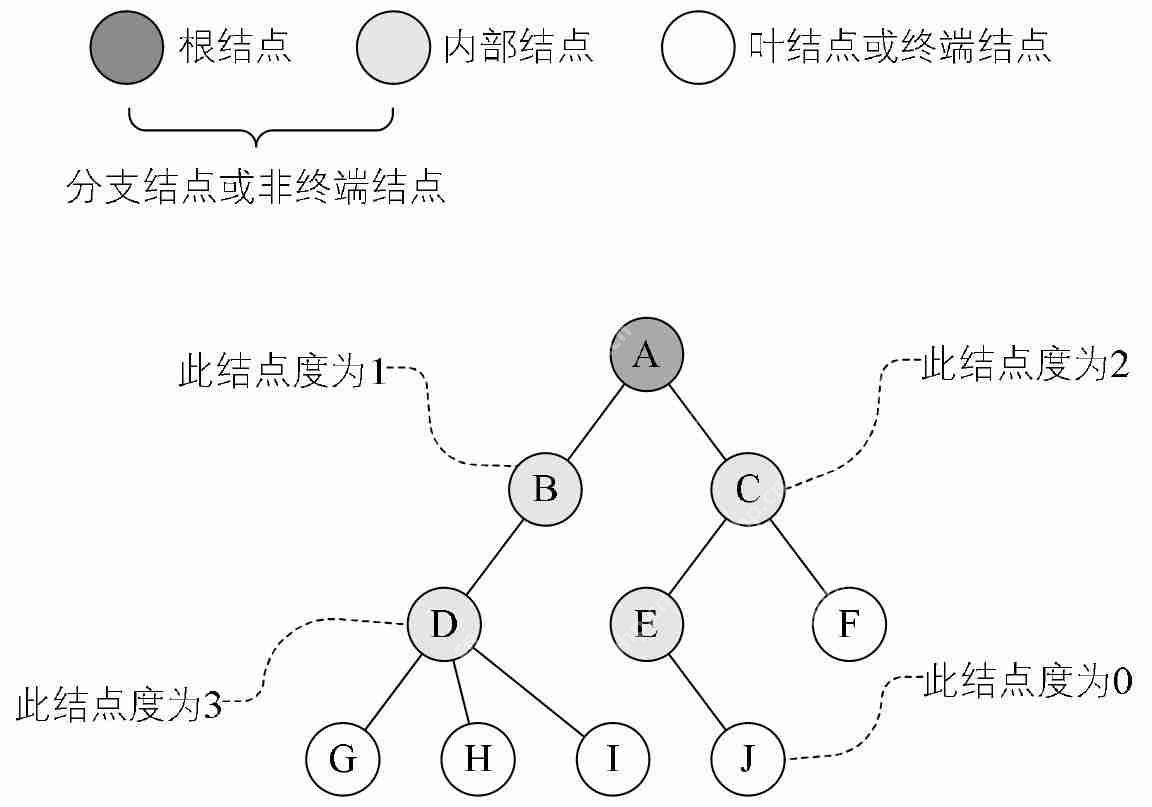
(1)不同的节点:根节点、内部节点、叶子节点以及节点的度
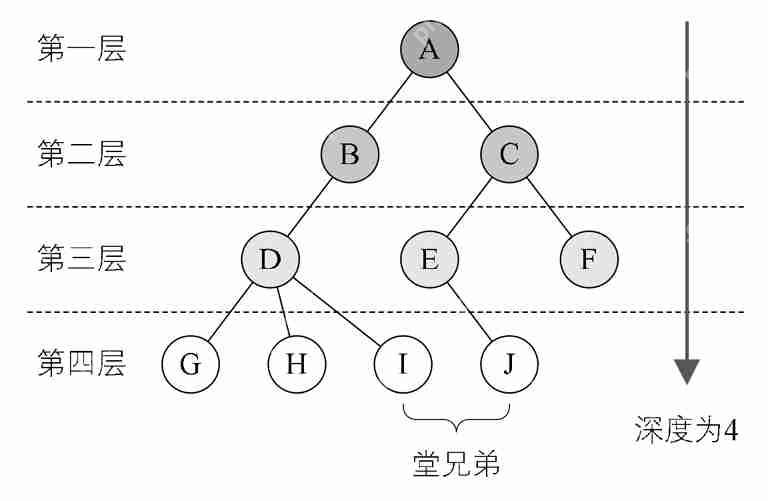
(2)节点的关系:双亲与孩子,爸爸回来了,爸爸去哪儿?
(3)节点的层次:结点的层次(Level)从根开始定义起,根为第一层,根的孩子为第二层。树中结点的最大层次称为树的深度(Depth)或高度。
回忆一下,当年某电视节目中会让游戏参与者猜一个产品的价格,如果参与者在限定时间内猜对了,那么他就可以获得这个产品。很多人都是一点点的提高数值来猜,但是这样猜会很没有效率。因此,很多聪明人都知道需要利用折半查找的思想去猜测。假定某个产品在100元的范围内,那么可以在7次之内猜出结果来,如下图所示:(由于是100以内的正整数,所以我们先猜50(100的一半),被告之“大了”,于是再猜25(50的一半),被告之“小了”,再猜37(25与50的中间数),小了,于是猜43,大了,40,大了,38,小了,39,完全正确。)
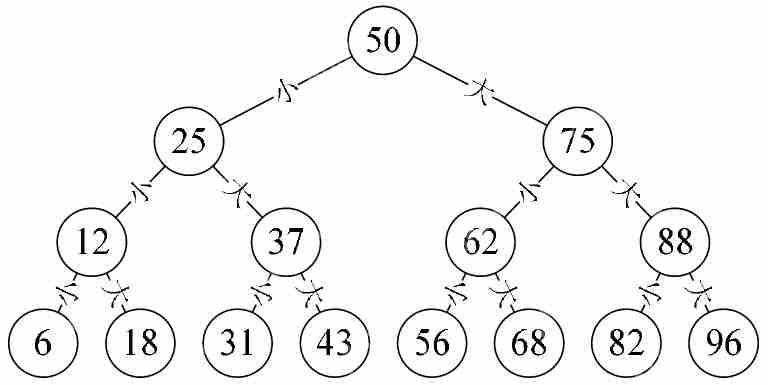
如上图所示,对于这种在某个阶段都是两种结果的情形,比如开和关、0和1、真和假、上和下、对与错,正面与反面等,都适合用树状结构来建模,而这种树是一种很特殊的树状结构,叫做二叉树。
2.2 二叉树的顺序存储结构二叉树的顺序存储结构就是用一维数组存储二叉树中的结点。结点的存储位置,也就是数组的下标要能体现结点之间的逻辑关系,比如双亲与孩子的关系,左右兄弟的关系等。
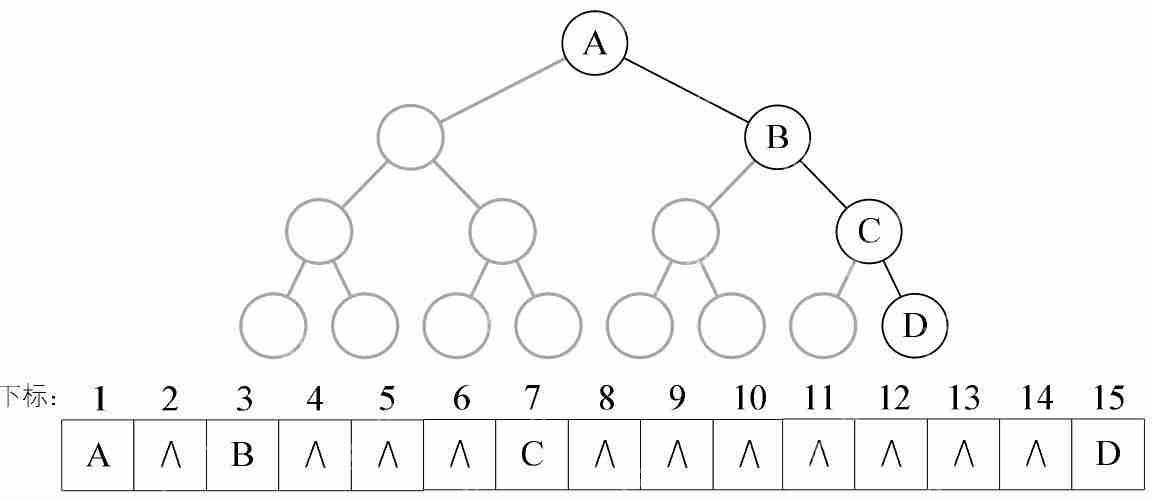
But,考虑一种极端的情况,一棵深度为k的右斜树,它只有k个结点,却需要分配2的k次方-1个存储单元空间,这显然是对存储空间的浪费,所以,顺序存储结构一般只适用于完全二叉树。
2.3 二叉树的链式存储结构既然顺序存储适用性不强,我们就要考虑链式存储结构。二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域是比较自然的想法,我们称这样的链表叫做二叉链表。其中data是数据域,lchild和rchild都是指针域,分别存放指向左孩子和右孩子的指针。
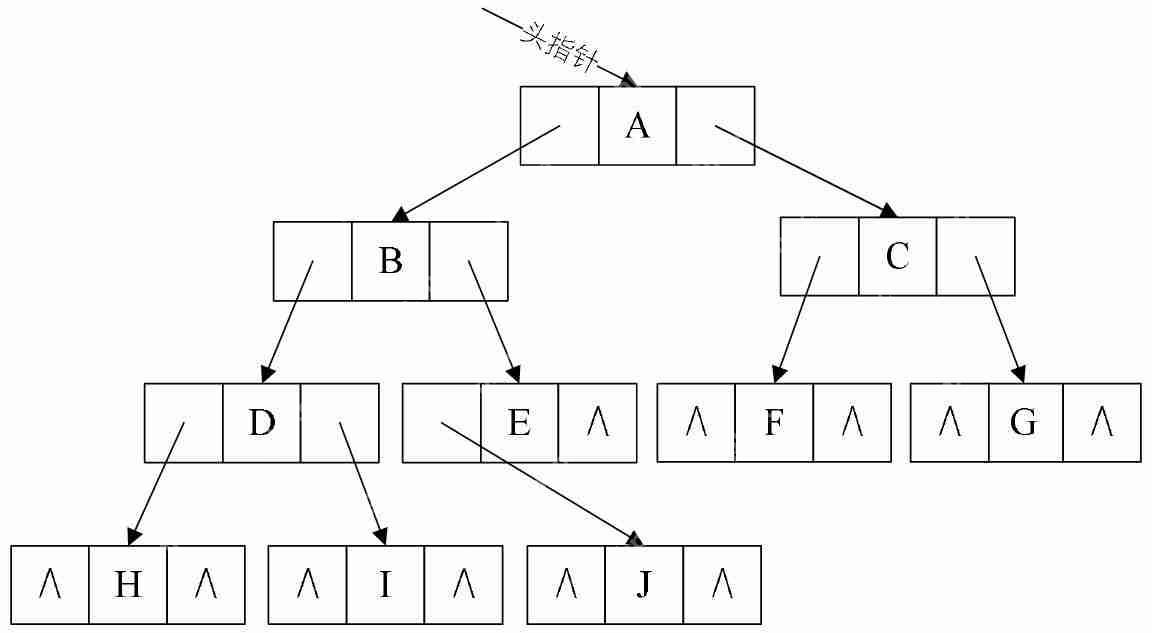
(1)二叉树节点的定义:
代码语言:javascript代码运行次数:0运行复制////// 二叉树的节点定义 /// ///数据具体类型 public class Node{ public T data { get; set; } public Node lchild { get; set; } public Node rchild { get; set; } public Node() { } public Node(T data) { this.data = data; } public Node(T data, Node lchild, Node rchild) { this.data = data; this.lchild = lchild; this.rchild = rchild; } }
(2)二叉树的创建实现:
代码语言:javascript代码运行次数:0运行复制 // Method01:判断该二叉树是否是空树 public bool IsEmpty() { return this.root == null; } // Method02:在节点p下插入左孩子节点的data public void InsertLeft(Node p, T data) { Node tempNode = new Node(data); tempNode.lchild = p.lchild; p.lchild = tempNode; } // Method03:在节点p下插入右孩子节点的data public void InsertRight(Node p, T data) { Node tempNode = new Node(data); tempNode.rchild = p.rchild; p.rchild = tempNode; } // Method04:删除节点p下的左子树 public Node RemoveLeft(Node p) { if (p == null || p.lchild == null) { return null; } Node tempNode = p.lchild; p.lchild = null; return tempNode; } // Method05:删除节点p下的右子树 public Node RemoveRight(Node p) { if (p == null || p.rchild == null) { return null; } Node tempNode = p.rchild; p.rchild = null; return tempNode; } 以上四个方法分别提供了新节点的插入以及移除的实现,我们可以针对某个节点进行插入左孩子有右孩子节点。
(3)二叉树的递归遍历:
首先我们通过几张图来看看二叉树的三种基本遍历:前序、中序以及后序遍历;
①前序遍历:若根节点不为空,则先访问根节点,然后先序遍历左子树,最后先序遍历右子树;

②中序遍历:若根节点不为空,则先中序遍历左子树,再访问根节点,最后中序遍历右子树;

③后序遍历:若根节点不为空,则首先后序遍历左子树,其次后序遍历右子树,最后访问根节点;
// Method01:前序遍历 public void PreOrder(Nodenode) { if (node != null) { // 根->左->右 Console.Write(node.data + " "); PreOrder(node.lchild); PreOrder(node.rchild); } } // Method02:中序遍历 public void MidOrder(Node node) { if (node != null) { // 左->根->右 MidOrder(node.lchild); Console.Write(node.data + " "); MidOrder(node.rchild); } } // Method03:后序遍历 public void PostOrder(Node node) { if (node != null) { // 左->右->根 PostOrder(node.lchild); PostOrder(node.rchild); Console.Write(node.data + " "); } }
本次实现采用了递归的方式实现遍历算法,主要是根据二叉树三种遍历(前序、中序以及后序遍历)的要求,依次输出各个节点的元素。至于非递归方式的遍历算法以及层次遍历算法会在下一篇中进行介绍。
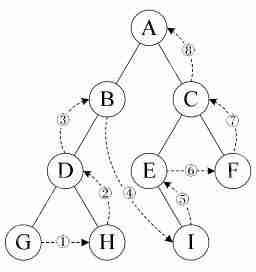
3.2 测试二叉树的遍历方法在上面的代码中,我们实现了二叉树的递归遍历算法,这里我们通过一段简单的测试代码来构造一颗二叉树,并进行遍历。首先,通过下图看看我们要创建的一颗二叉树是什么鬼?
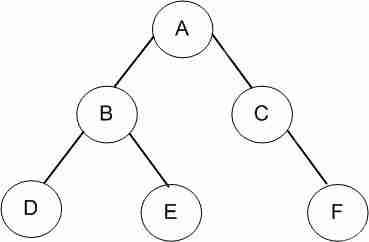
(1)测试代码:
代码语言:javascript代码运行次数:0运行复制 static void MyBinaryTreeBasicTest() { // 构造一颗二叉树,根节点为"A" MyBinaryTree bTree = new MyBinaryTree("A"); Node rootNode = bTree.Root; // 向根节点"A"插入左孩子节点"B"和右孩子节点"C" bTree.InsertLeft(rootNode, "B"); bTree.InsertRight(rootNode, "C"); // 向节点"B"插入左孩子节点"D"和右孩子节点"E" Node nodeB = rootNode.lchild; bTree.InsertLeft(nodeB, "D"); bTree.InsertRight(nodeB, "E"); // 向节点"C"插入右孩子节点"F" Node nodeC = rootNode.rchild; bTree.InsertRight(nodeC, "F"); // 前序遍历 Console.WriteLine("---------PreOrder---------"); bTree.PreOrder(bTree.Root); // 中序遍历 Console.WriteLine(); Console.WriteLine("---------MidOrder---------"); bTree.MidOrder(bTree.Root); // 后序遍历 Console.WriteLine(); Console.WriteLine("---------PostOrder---------"); bTree.PostOrder(bTree.Root); } (2)运行结果:
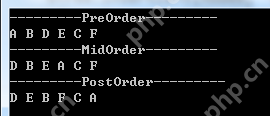
本文实现的C#版二叉树参考代码下载:http://pan.baidu.com/s/1eQ1xmXs
参考资料(1)程杰,《大话数据结构》
(2)陈广,《数据结构(C#语言描述)》
(3)段恩泽,《数据结构(C#语言版)》
(4)杨俊明,《数据结构C#版笔记—树与二叉树》
(5)Frank Fan,《万丈高楼平地起之C#实现二叉树操作》
作者:周旭龙
出处:http://edisonchou.cnblogs.com
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文链接。






























