1. 树型结构
1.1概念
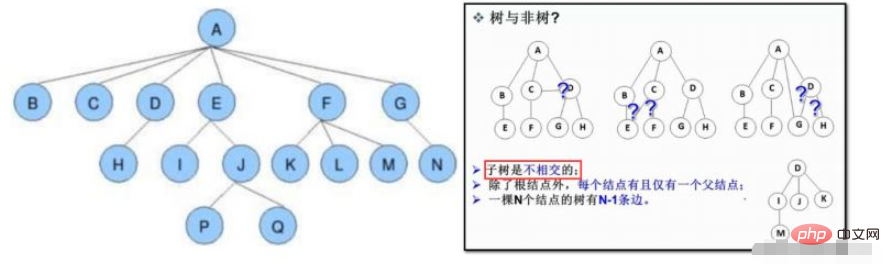
树是一种 非线性 的数据结构,它是由 n ( n>=0 )个有限结点组成一个具有层次关系的集合。 把它叫做树是因为它看 起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的 。
1.2 概念(重要)
a.节点的度:该节点子树的个数;如上图:A的度为6,J的度为2
b.树的度:该树中,最大结点的度就是该数的度;如上图:树的度为6
c.叶子节点(终端节点):度为0的节点(没有子树的节点)
立即学习“Java免费学习笔记(深入)”;
d.双亲结点/父节点:如上图:D是H的父节点
孩子节点/子节点:如上图:H是D的子节点
e.根节点:没有双亲的节点;如上图:A
f.节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
g.树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
2. 二叉树(重点)
2.1 概念
每个节点最多只有两颗子树,度
2.2 二叉树的基本形态
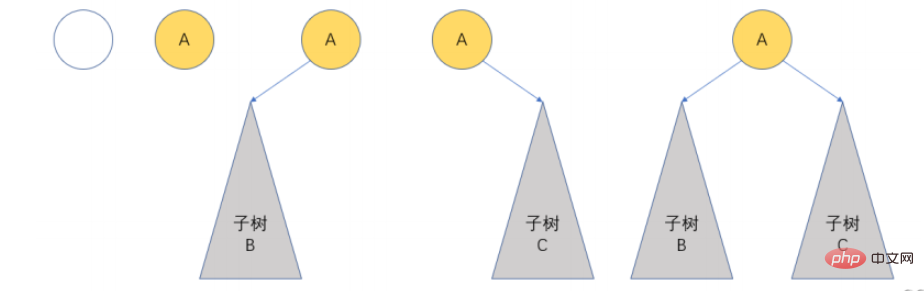
2.3 两种特殊的二叉树
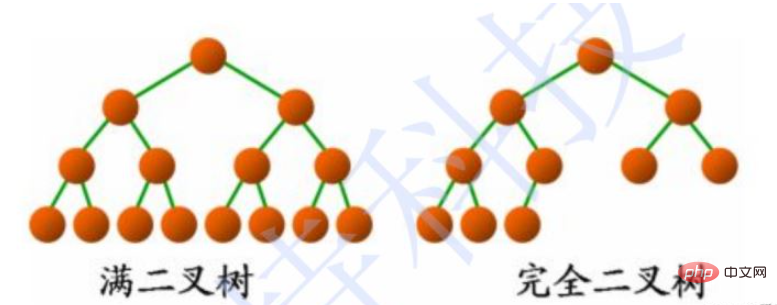
a.满二叉树:非子叶度都为2
b.完全二叉树:满二叉树缺了“右下角”
2.4 二叉树的性质
a.满二叉树
1.高度为K,则有2^k-1个节点
2.层次为K,则该层有2^(k-1)个节点
3.边个数 = 节点个数 - 1
4.度为0有n0个,度为2有n2个,则 n0 = n2 + 1
b.完全二叉树
1.有右孩子必有左孩子
2.只可能有一个度为1的节点
2.5 二叉树的存储
二叉树的存储结构分为:顺序存储和类似于链表的链式存储。
顺序存储:只能存完全二叉树
链式存储:普通二叉树
本次展示链式存储
二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式 ,
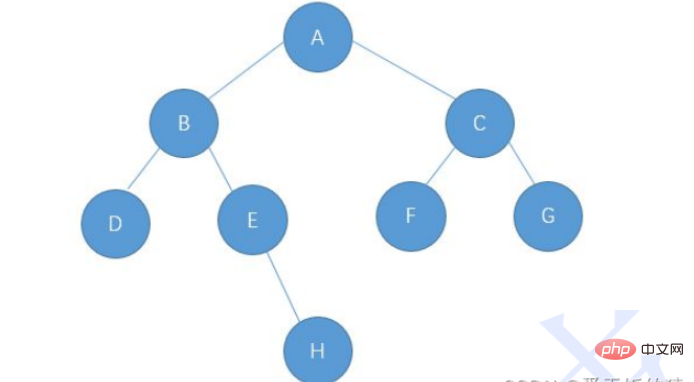
以此图为例, 具体如下:
// 孩子表示法
private static class TreeNode{
char val;
TreeNode left;
TreeNode right;
public TreeNode(char val) {
this.val = val;
}
}初始化:
public static TreeNode build(){
TreeNode nodeA=new TreeNode('A');
TreeNode nodeB=new TreeNode('B');
TreeNode nodeC=new TreeNode('C');
TreeNode nodeD=new TreeNode('D');
TreeNode nodeE=new TreeNode('E');
TreeNode nodeF=new TreeNode('F');
TreeNode nodeG=new TreeNode('G');
TreeNode nodeH=new TreeNode('H');
nodeA.left=nodeB;
nodeA.right=nodeC;
nodeB.left=nodeD;
nodeB.right=nodeE;
nodeE.right=nodeH;
nodeC.left=nodeF;
nodeC.right=nodeG;
return nodeA;
}2.6 二叉树的基本操作
2.6.1 二叉树的遍历 (递归)
1. NLR :前序遍历 (Preorder Traversal 亦称先序遍历 )—— 访问根结点 ---> 根的左子树 ---> 根的右子树。
//先序遍历 : 根左右
public static void preOrder(TreeNode root){
if(root==null){
return;
}
System.out.print(root.val+" ");
preOrder(root.left);
preOrder(root.right);
}2. LNR :中序遍历 (Inorder Traversal)—— 根的左子树 ---> 根节点 ---> 根的右子树。
//中序遍历
public static void inOrder(TreeNode root){
if(root==null){
return;
}
preOrder(root.left);
System.out.print(root.val+" ");
preOrder(root.right);
}3. LRN :后序遍历 (Postorder Traversal)—— 根的左子树 ---> 根的右子树 ---> 根节点。
//后序遍历
public static void postOrder(TreeNode root){
if(root==null){
return;
}
preOrder(root.left);
preOrder(root.right);
System.out.print(root.val+" ");
}2.6.2 二叉树的遍历 (迭代)
1.前序遍历
//方法2(迭代)
//先序遍历 (迭代)
public static void preOrderNonRecursion(TreeNode root){
if(root==null){
return ;
}
Deque stack=new LinkedList<>();
stack.push(root);
while (!stack.isEmpty()){
TreeNode cur=stack.pop();
System.out.print(cur.val+" ");
if(cur.right!=null){
stack.push(cur.right);
}
if(cur.left!=null){
stack.push(cur.left);
}
}
} 2.中序遍历
//方法2(迭代)
//中序遍历 (迭代)
public static void inorderTraversalNonRecursion(TreeNode root) {
if(root==null){
return ;
}
Deque stack=new LinkedList<>();
// 当前走到的节点
TreeNode cur=root;
while (!stack.isEmpty() || cur!=null){
// 不管三七二十一,先一路向左走到根儿~
while (cur!=null){
stack.push(cur);
cur=cur.left;
}
// 此时cur为空,说明走到了null,此时栈顶就存放了左树为空的节点
cur=stack.pop();
System.out.print(cur.val+" ");
// 继续访问右子树
cur=cur.right;
}
} 3.后序遍历
//方法2(迭代)
//后序遍历 (迭代)
public static void postOrderNonRecursion(TreeNode root){
if(root==null){
return;
}
Deque stack=new LinkedList<>();
TreeNode cur=root;
TreeNode prev=null;
while (!stack.isEmpty() || cur!=null){
while (cur!=null){
stack.push(cur);
cur=cur.left;
}
cur=stack.pop();
if(cur.right==null || prev==cur.right){
System.out.print(cur.val+" ");
prev=cur;
cur=null;
}else {
stack.push(cur);
cur=cur.right;
}
}
} 2.6.3 二叉树的基本操作
1.求结点个数(递归&迭代)
//方法1(递归)
//传入一颗二叉树的根节点,就能统计出当前二叉树中一共有多少个节点,返回节点数
//此时的访问就不再是输出节点值,而是计数器 + 1操作
public static int getNodes(TreeNode root){
if(root==null){
return 0;
}
return 1+getNodes(root.left)+getNodes(root.right);
}
//方法2(迭代)
//使用层序遍历来统计当前树中的节点个数
public static int getNodesNoRecursion(TreeNode root){
if(root==null){
return 0;
}
int size=0;
Deque queue=new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
size++;
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
return size;
} 2.求叶子结点个数(递归&迭代)
//方法1(递归)
//传入一颗二叉树的根节点,就能统计出当前二叉树的叶子结点个数
public static int getLeafNodes(TreeNode root){
if(root==null){
return 0;
}
if(root.left==null && root.right==null){
return 1;
}
return getLeafNodes(root.left)+getLeafNodes(root.right);
}
//方法2(迭代)
//使用层序遍历来统计叶子结点的个数
public static int getLeafNodesNoRecursion(TreeNode root){
if(root==null){
return 0;
}
int size=0;
Deque queue=new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()){
TreeNode cur=queue.poll();
if(cur.left==null && cur.right==null){
size++;
}
if(cur.left!=null){
queue.offer(cur.left);
}
if(cur.right!=null){
queue.offer(cur.right);
}
}
return size;
} 3.求第 k 层结点个数
//求出以root为根节点的二叉树第k层的节点个数
public static int getKLevelNodes(TreeNode root,int k){
if(root==null || k<=0){
return 0;
}
if(k==1){
return 1;
}
return getKLevelNodes(root.left,k-1)+getKLevelNodes(root.right,k-1);
}4.求树的高度
//传入一个以root为根节点的二叉树,就能求出该树的高度
public static int height(TreeNode root){
if(root==null){
return 0;
}
return 1+ Math.max(height(root.left),height(root.right));
}5.判断二叉树数中是否存在值为value的节点
//判断当前以root为根节点的二叉树中是否包含指定元素val,
//若存在返回true,不存在返回false
public static boolean contains(TreeNode root,char value){
if(root==null){
return false;
}
if(root.val==value){
return true;
}
return contains(root.left,value) || contains(root.right,value);
}2.7 二叉树的层序遍历
//层序遍历
public static void levelOrder(TreeNode root) {
if(root==null){
return ;
}
// 借助队列来实现遍历过程
Deque queue =new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()){
int size=queue.size();
for (int i = 0; i < size; i++) {
TreeNode cur=queue.poll();
System.out.print(cur.val+" ");
if(cur.left!=null){
queue.offer(cur.left);
}
if(cur.right!=null){
queue.offer(cur.right);
}
}
}
} 






























