mahout提供一些可扩展的机器学习领域经典算法的实现,旨在帮助开发人员更加方便快捷地创建智能应用程序。mahout包含许多实现,包括聚类、分类、推荐过滤、频繁子项挖掘。此外,通过使用 apache hadoop 库,mahout 可以有效地扩展到云中。

该老师讲课风格:
教师讲课深入浅出,条理清楚,层层剖析,环环相扣,论证严密,结构严谨,用思维的逻辑力量吸引学生的注意力,用理智控制课堂教学进程。学生通过听教师的讲授,不仅学到知识,也受到思维的训练,还受到教师严谨的治学态度的熏陶和感染
本视频中较为难点是逻辑回归分类器_贝叶斯分类器_1了:
1.背景
首先,在文章的开头,先提出几个问题,如果这些问题你都答得上来,那么本文你就无需阅读了,或者你阅读的动机纯粹是给本文挑毛病,当然我也无比欢迎,请发送邮件“毛病の朴素贝叶斯”发送至297314262@qq.com,我会认真阅读你的来信。
By the way,如果阅读完本文,你还是无法回答以下问题,那么也请你邮件通知我,我会尽量解答你的疑惑。
朴素贝叶斯分类器中的“朴素”特指此分类器的什么特性
朴素贝叶斯分类器与极大似然估计(MLE)、最大后验概率(MAP)的关系
朴素贝叶斯分类、逻辑回归分类,生成模型、判决模型的关系
有监督学习和贝叶斯估计的关系
2.约定
那么,本文开始。首先,关于本文可能出现的各种表达形式,在此做一番约定
大写字母,如X,表示随机变量;如果X是多维变量,那么下标i表示第i维变量,即Xi
小写字母,如Xij,表示变量的一种取值(Xi的第j种取值)
3.贝叶斯估计与有监督学习
好的,那么首先回答第4个问题,如何用贝叶斯估计解决有监督学习问题?
对于有监督学习,我们的目标实际上是估计一个目标函数f : X->Y,,或目标分布P(Y|X),其中X是样本的各个feature组成的多维变量,Y是样本的实际分类结果。假设样本X的取值为xk,那么,根据贝叶斯定理,分类结果为yi的概率应该为:
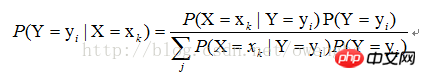
因此,要估计P(Y=yi|X=xk),只要根据样本,求出P(X=xk|Y=yi)的所有估计,以及P(Y=yi)的所有估计,就可以了。此后的分类过程,就是求另P(Y=yi|X=xk)最大的那个yi就可以了。那么由此可见,利用贝叶斯估计,可以解决有监督学习的问题。
4.分类器的“朴素”特性
接下来,回答第1个问题,何为“朴素”?
从第3节的分析里,我们知道,要求得P(Y=yi|X=xk),就需要知道P(X=xk|Y=yi)的所有估计,以及P(Y=yi)的所有估计,那么假设X为N维变量,其每一维变量都有两种取值(如文本分类中常见的各个term出现与否对应的取值0/1),而Y也有两种类别,那么就需要求出2*(2^N - 1)个估计(注意,由于在给定Y为某一类别的情况下,X的各个取值的概率和为1,所以实际需要估计的值为2^N - 1)。可以想象,对于N很大的情况(文本分类时,term的可能取值是非常大的),这一估计的计算量是巨大的。那么如何减少需要估计的量,而使得贝叶斯估计方法具有可行性呢?这里,就引入一种假设:
假设:在给定Y=yi的条件下,X的各维变量彼此相互独立。
那么,在这一假设的条件下,P(X=xk|Y=yi)=P(X1=x1j1|Y=yi)P(X2=x2j2|Y=yi)...P(Xn=xnjn|Y=yi),也就是说,此时只需要求出N个估计就可以了。因此,这一假设将贝叶斯估计的计算量从2*(2^N - 1)降为了N,使这一分类器具有了实际可行性。那么这一假设就成为朴素特性。
5.极大似然估计和最大后验概率解
接下来,回答第2个问题,首选我们将极大似然估计法应用于朴素贝叶斯分类器的求解过程。
上面说了,P(X=xk|Y=yi)的求解,可以转化为对P(X1=x1j1|Y=yi)、P(X2=x2j2|Y=yi)、... P(Xn=xnjn|Y=yi)的求解,那么如何利用极大似然估计法求这些值呢?
首选我们需要理解什么是极大似然估计,实际上,在我们的概率论课本里,关于极大似然估计的讲解,都是在解决无监督学习问题,而看完本节内容后,你应该明白,在朴素特性下,用极大似然估计解决有监督学习问题,实际上就是在各个类别的条件下,用极大似然估计解决无监督学习问题。






























