范畴论中的满态射是右可消去的态射,它在不同范畴中泛化了“覆盖”概念,如在集合范畴中等价于满射函数,而在拓扑空间范畴中对应像集稠密的连续映射,体现了通过态射关系而非元素来刻画结构本质的思想。
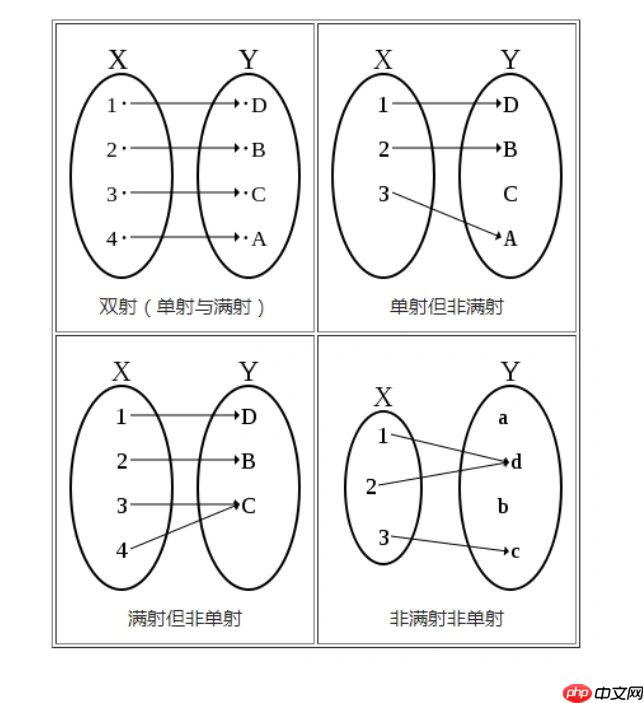
在范畴论的语境下,我们谈论的“满射”不再仅仅是集合论中那个直观的“覆盖”概念。它的特殊意义,在于它超越了元素层面,转而关注态射(morphism)在整个范畴结构中的行为与作用。简单来说,范畴论中的满射,即“满态射”(epimorphism),是一种右可消去(right-cancellable)的态射,它更深刻地揭示了对象之间的结构关联,而非仅仅是其内部元素的映射关系。
解决方案
当我们从集合论的视角来看待一个函数 $f: A \to B$ 是满射,我们通常指的是 $B$ 中的每一个元素 $b$ 都能在 $A$ 中找到至少一个原像 $a$,使得 $f(a) = b$。这是一种非常具体且依赖于“元素”存在的定义。然而,在范畴论中,我们的对象不一定有“元素”——它们可以是群、拓扑空间、向量空间,甚至是更抽象的结构,其间只有“态射”连接。
范畴论为了泛化这一概念,引入了“满态射”:一个态射 $f: A \to B$ 被称为满态射,如果对于任意对象 $C$ 和任意两个不同的态射 $g_1, g_2: B \to C$,只要 $g_1 \circ f = g_2 \circ f$,就必然有 $g_1 = g_2$。换句话说,如果 $f$ 后面接的两个态射在复合后变得无法区分,那么这两个态射本身就必须是同一个。这表明 $f$ 在“区分”后续态射方面具有某种“完全性”或“覆盖性”。它强调的是 $f$ 在态射复合链中的作用,而非其“内部”元素的映射。
这种定义的美妙之处在于其普适性。它不再要求我们深入对象的内部去检查元素,而是让我们通过其与其他态射的交互来理解其性质。这是一种从外部、从关系出发的定义,它捕获了“满射”在更广阔数学语境中的本质。
满态射与集合论满射:核心差异与深远影响
满态射(epimorphism)与集合论中的满射函数(surjective function)之间存在着微妙但至关重要的区别。在某些范畴中,它们确实是等价的,但这并非普遍规律,而这种不一致正是范畴论洞察力的体现。
在集合范畴(Set)中,对象是集合,态射是函数。一个函数是满态射当且仅当它是集合论意义上的满射。这很好理解,如果 $f: A \to B$ 是一个集合论满射,那么 $B$ 中的每个元素都是 $f$ 的像。任何从 $B$ 出发的两个不同函数 $g_1, g_2: B \to C$ 必然会在 $B$ 的某个元素 $b$ 上取不同值。由于 $b$ 有原像 $a \in A$,那么 $g_1(f(a)) \neq g_2(f(a))$,所以 $g_1 \circ f \neq g_2 \circ f$。反之亦然。
然而,一旦我们跳出 Set 范畴,情况就变得有趣了。例如,在拓扑空间范畴(Top)中,对象是拓扑空间,态射是连续映射。一个连续映射 $f: X \to Y$ 是满态射,当且仅当其像 $f(X)$ 在 $Y$ 中是稠密的。这意味着 $f(X)$ 不必覆盖整个 $Y$。一个经典的例子是包含映射 $i: \mathbb{Q} \to \mathbb{R}$(有理数到实数,带有子空间拓扑)。这个映射显然不是集合论意义上的满射,因为 $\mathbb{R}$ 中有无理数没有原像。但它是一个满态射,因为 $\mathbb{Q}$ 在 $\mathbb{R}$ 中是稠密的。任何两个从 $\mathbb{R}$ 出发的连续映射 $g_1, g_2: \mathbb{R} \to Z$ 如果在 $\mathbb{Q}$ 上一致,那么由于连续性,它们在 $\mathbb{R}$ 上也必须一致。
另一个例子是在环范畴(Rng,带有单位元且保持单位元的环同态)中。包含映射 $j: \mathbb{Z} \to \mathbb{Q}$(整数环到有理数域)是一个满态射,但它同样不是集合论意义上的满射。如果 $g_1, g_2: \mathbb{Q} \to R$ 是环同态,且 $g1|{\mathbb{Z}} = g2|{\mathbb{Z}}$,那么对于任意 $p/q \in \mathbb{Q}$(其中 $q \neq 0$),我们有 $g_1(p/q) = g_1(p) \cdot g_1(q)^{-1}$。由于 $p, q \in \mathbb{Z}$,我们知道 $g_1(p) = g_2(p)$ 和 $g_1(q) = g_2(q)$。因此 $g_1(p/q) = g_2(p/q)$,即 $g_1 = g_2$。
这些差异之所以重要,是因为它们揭示了范畴论的深层哲学:它关注的是结构和结构保持映射之间的关系,而不是对象的内部构造。满态射的定义允许我们在没有“元素”概念的范畴中,依然能够捕获到“覆盖”或“生成”的本质,这极大地扩展了数学工具的适用范围。
满态射如何在不同数学结构中泛化“覆盖”概念?
满态射的定义方式,使其能够以一种与具体数学结构无关的方式,泛化了“覆盖”这一核心思想。它不再拘泥于集合论的直观,而是从行为模式上统一了不同数学领域中“onto”的含义。
群范畴(Grp): 对象是群,态射是群同态。在这个范畴中,满态射恰好就是满射群同态。如果一个群同态 $f: G \to H$ 是满射,那么 $f(G) = H$,任何从 $H$ 出发的两个不同同态 $g_1, g_2: H \to K$ 必然能被 $f$ 区分。反之,如果 $f$ 不是满射,那么 $f(G)$ 是 $H$ 的一个真子群。我们可以构造两个不同的同态 $g_1, g_2: H \to K$(例如,一个将 $H$ 映射到某个群的单位元,另一个则不是),使得它们在 $f(G)$ 上一致,但在 $H$ 的其他元素上不同。
模范畴(Mod_R): 对象是 $R$-模,态射是模同态。与群范畴类似,模范畴中的满态射也恰好是满射模同态。这得益于模的丰富代数结构,使得“元素”层面的满射与“态射行为”层面的满态射保持了一致。
代数几何中的例子: 在代数几何中,一个态射 $f: X \to Y$(例如,环谱之间的态射)是满态射,如果它在拓扑空间层面上是满射,并且对于每个 $Y$ 中的点 $y$,诱导出的局部环态射是满射的。这比简单的拓扑满射更强,它结合了拓扑和代数结构的信息。
这些例子说明,满态射的定义是如此精妙,它能够根据具体范畴的“规则”(即态射的性质),自动调整其“覆盖”的含义。在集合和代数范畴中,由于态射的结构足够“强”,元素层面的覆盖与态射行为层面的覆盖一致。而在拓扑或环范畴中,由于态射的限制(连续性、环同态性),“覆盖”的意义就变得更加微妙,它可能意味着“稠密”或“在分数域上一致”等。这正是范畴论的强大之处,它提供了一个统一的语言来讨论这些看似不同的现象。
运用满态射概念的实际价值与深层洞察
理解和运用满态射的概念,不仅仅是理论上的严谨,它为我们带来了多方面的实际价值和更深层次的数学洞察。
首先,抽象与统一性是其最显著的优点。满态射提供了一个统一的框架,让我们可以在不同的数学分支中讨论“覆盖”或“onto”的属性,而无需每次都重新定义。这种抽象能力使得数学家能够发现不同领域之间的深层联系,并借用一个领域的工具来解决另一个领域的问题。例如,同调代数中的精确序列,其定义就大量依赖于满态射和单态射(monomorphism,满态射的对偶概念)。
其次,对偶性思维是范畴论的核心,满态射正是这种思维的完美体现。满态射是单态射的对偶。一个态射 $f: A \to B$ 是单态射,如果对于任意对象 $C$ 和任意两个不同的态射 $g_1, g_2: C \to A$,只要 $f \circ g_1 = f \circ g_2$,就必然有 $g_1 = g_2$。这意味着 $f$ 是左可消去的。这种对偶性不仅优雅,而且在证明和构造中提供了强大的工具。如果一个定理对单态射成立,那么通过对偶原理,我们可以尝试推导其对满态射的相应结论。
再者,满态射在泛性质(Universal Properties)的构造中扮演着关键角色。许多重要的数学构造,如商对象、余积、上极限等,都伴随着一个满足泛性质的满态射。例如,给定一个等价关系 $R$ 在集合 $A$ 上,商集 $A/R$ 伴随着一个规范的满射 $q: A \to A/R$,这个满射是“泛”的,意味着任何从 $A$ 出发且尊重 $R$ 的函数 $f: A \to B$ 都能唯一地通过 $A/R$ 因子化,即存在唯一的 $h: A/R \to B$ 使得 $f = h \circ q$。满态射在这里确保了 $A/R$ 是“最小的”能够承载这种因子化的对象。
最后,满态射促使我们重新审视数学概念的本质。它教会我们,一个数学概念的真正意义可能不在于其内部结构的细节,而在于它在更广阔的数学结构网络中扮演的角色。通过关注态射的复合行为,我们能够更深刻地理解对象之间的关系,从而获得更纯粹、更具普适性的数学洞察。这是一种从“关系”而非“实体”出发的思考方式,它为现代数学的发展提供了强大的抽象工具。






























