二叉树可用于实现二叉查找树和二叉堆,在计算机科学中,二叉树是每个结点最多有两个子树的树结构,通常子树被称作“左子树”和“右子树”,根据不同的用途可分为:1、完全二叉树;2、满二叉树;3、平衡二叉树。

二叉树的作用
二叉树常被用于实现二叉查找树和二叉堆。
在计算机科学中,二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”和“右子树”。
根据不同的用途可分为:
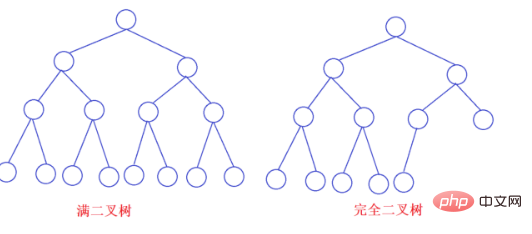
1、完全二叉树——若设二叉树的高度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第h层有叶子结点,并且叶子结点都是从左到右依次排布,这就是完全二叉树。
2、满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。
beta v1.1版本为第一个版本,简单的整合了基础功能,各位站长拿到程序后,不要纠结后台的功能简单,后续将不断更新扩展。在beta v1.1版本使用过程中遇到什么问题,请登录 www.loftto.com 进行反馈! 安装说明######重要提醒:程序不支持二级目录安装,请使用一级目录或二级目录绑定!#第一步,确定你的服务器支持PHP+mysql。#第二步,确定你的服务器开启了gd库。#第三步,
 0
0

3、平衡二叉树——平衡二叉树又被称为AVL树(区别于AVL算法),它是一棵二叉排序树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
扩展资料
深度为h的二叉树最多有个结点(h>=1),最少有h个结点。对于任意一棵二叉树,如果其叶结点数为N0,而度数为2的结点总数为N2,则N0=N2+1。
有N个结点的完全二叉树各结点如果用顺序方式存储,则结点之间有如下关系为若I为结点编号则 如果I>1,则其父结点的编号为I/2。如果2*I<=N,则其左孩子(即左子树的根结点)的编号为2*I。若2*I>N,则无左孩子。如果2*I+1<=N,则其右孩子的结点编号为2*I+1。
以上就是二叉树有什么用的详细内容,更多请关注php中文网其它相关文章!

每个人都需要一台速度更快、更稳定的 PC。随着时间的推移,垃圾文件、旧注册表数据和不必要的后台进程会占用资源并降低性能。幸运的是,许多工具可以让 Windows 保持平稳运行。

Copyright 2014-2025 https://www.php.cn/ All Rights Reserved | php.cn | 湘ICP备2023035733号